Diodati.org - Accessibilità e traduzioni dal W3C

di Michele Diodati

Una carrellata senza pretese di completezza sui principali algoritmi di compressione delle immagini grafiche e sulle caratteristiche di alcuni dei principali formati di file che li incorporano, con un occhio particolare ai formati destinati al Web e al futuro che ci aspetta (JPEG 2000).

 La compressione secondo zio Paperone 

Ricordo un fumetto letto da bambino tanti anni fa. Ecco la storia: zio Paperone ha escogitato una straordinaria speculazione edilizia; grazie ad una mirabolante invenzione di Archimede Pitagorico, può costruire dei palazzi apparentemente normali visti dall'esterno, ma dotati della proprietà di rimpicciolire a dimensioni minuscole qualsiasi persona o cosa vi entri, salvo far loro riacquistare le proporzioni naturali quando compiono il percorso inverso ed escono nuovamente sulla strada. Così, visti da dentro, i palazzi di zio Paperone sono degli immensi grattacieli, i cui numerosissimi abitanti, nel passaggio dal mondo esterno alla ridotta realtà interna, conservano intatte le loro caratteristiche individuali.

E il papero più ricco e avaro del mondo può continuare ad accumulare ricchezze, grazie al rapporto per lui estremamente vantaggioso tra il costo dei terreni acquistati e l'incasso ricavato dalle vendite della moltitudine di appartamenti esistenti all'interno dei palazzi.

Che cos'è questa storia - ho riflettuto molti anni dopo - se non la miglior metafora possibile del concetto di compressione?

La compressione è appunto questo: l'atto di ridurre lo spazio occupato da un oggetto, agendo sugli elementi costitutivi dell'oggetto stesso.

Ma in termini informatici ciò significa che l'oggetto è un file o un insieme di file, e cioè un insieme di bit. Dal che consegue che comprimere un oggetto simile - costituito unicamente da una quantità finita di 1 e di 0 - non può significare altro che diminuire il numero di 1 e di 0, ovvero di bit, che lo compongono.

Tale operazione è sostanzialmente differente dai tipi di compressione che possiamo osservare nel mondo fisico, ad esempio dalla compressione che una pressa effettua sulla carcassa di un'automobile. In questo caso, infatti, la quantità di materia di cui è costituita l'automobile non diminuisce a causa dell'azione della pressa: finisce semplicemente per occupare meno spazio, diventando allo stesso tempo più densa. Potremmo dire, semplificando, che il numero di particelle di cui è costituita l'auto rimane invariato, mentre varia - diminuendo in modo inversamente proporzionale alla pressione applicata - lo spazio che le separa.

I bit che costituiscono un file, invece, non si avvicinano tra loro in seguito alla compressione, diventando, che so, "bittìni". Diminuiscono piuttosto di numero.

E' chiaro quindi che la compressione, in ambito informatico, è tutt'altra cosa rispetto al concetto intuitivo di compressione a cui siamo abituati, legato all'applicazione di una o più forze tendenti a ridurre lo spazio occupato da un oggetto.

La forza che occorre per comprimere un file è la forza del pensiero. Ovviamente non nel senso di telecinesi, ma nel senso di calcolo matematico. L'insieme dei calcoli aventi per scopo la riduzione delle dimensioni di un file o di un insieme di file prende il nome di algoritmo di compressione (in generale, nel linguaggio informatico, si definisce algoritmo una serie di operazioni logiche e algebriche, espresse in un linguaggio comprensibile all'elaboratore, la cui sequenza costituisce un programma).

 Reversibilità e ibernazione 

Pensiamo ora ad un tipico file grafico, ad esempio una fotografia a colori salvata in modalità RGB. Senza addentrarci in discorsi complessi sulla codifica del colore, diremo che questa modalità richiede l'uso di tre byte per memorizzare le informazioni di colore e luminosità relative a ciascun punto - o pixel - dell'immagine. Per sapere, quindi, quanto spazio occupa su disco questo file grafico, ci basta moltiplicare per tre il numero complessivo di punti da cui è costituita l'immagine. Questo numero si ottiene, a sua volta, moltiplicando il numero delle colonne per il numero delle righe che compongono il rettangolo occupato dall'immagine.

Data allora una foto di 1024 pixel orizzontali per 768 verticali, lo spazio che essa occupa come file su disco è di 1024 x 768 x 3 = 2.359.296 byte, il che equivale a 2.304 Kilobyte o, ancora, a 2,25 Megabyte. E' importante precisare che tale cifra rappresenta lo spazio occupato dal file grafico in forma non compressa.

Un qualsiasi programma per la visualizzazione di immagini a monitor avrà bisogno di tutti quei byte per poter generare sullo schermo del computer una foto uguale all'originale memorizzato su disco. E non solo i byte dovranno esserci tutti, ma dovranno anche risultare disposti nella stessa esatta sequenza in cui sono stati la prima volta archiviati.

Ma se è compito specifico di un algoritmo di compressione trasformare la sequenza di byte che costituisce un file in una differente sequenza più breve, è evidente che la sequenza di byte che compone un file grafico compresso non sarà utilizzabile per generare l'immagine contenuta nel file originale.

Ciò ci porta a definire una caratteristica fondamentale di qualsiasi formato di compressione passibile di applicazioni pratiche: la reversibilità della compressione. In genere, se un programma ha la capacità di salvare un file in un formato compresso, è anche in grado di leggere i file che sono stati compressi con quel particolare formato, ripristinando l'informazione in essi contenuta, cioè decomprimendoli.

Senza reversibilità, anche il migliore degli algoritmi di compressione è inutile, come lo è farsi ibernare oggi da vivi, non sapendo se un domani si potrà essere scongelati e riportati ad una vita normale.

 Fedeltà assoluta e fedeltà relativa 

In virtù di quanto detto sopra, la principale differenza che possiamo stabilire tra i formati di compressione delle immagini grafiche è data dalla misura della loro reversibilità. Un formato che è in grado di restituire, al termine della decompressione, un'immagine esattamente uguale - pixel per pixel - all'originale com'era prima che venisse compresso, viene normalmente definito con l'impronunciabile termine inglese lossless. In italiano potremmo tradurre con senza perdita oppure con non distruttivo. Viceversa, un formato di compressione che non può assicurare una reversibilità assoluta, viene definito in inglese lossy, ovvero, in italiano, con perdita o anche distruttivo. La cosa che si perde o non si perde è la fedeltà all'originale dell'immagine ripristinata.

I grafici e gli impaginatori di professione devono conoscere perfettamente le caratteristiche dei formati di compressione che adoperano, se vogliono ottenere il meglio dalle manipolazioni che effettuano sui file. Sarebbe infatti un grave errore salvare e risalvare un file in un formato lossy come il JPG, per poi utilizzarlo alla fine in un formato "senza perdita" come il TIF. E' invece corretto fare il contrario, ovvero salvare quante volte si vuole un lavoro in corso d'opera in un formato non distruttivo, per poi salvarlo solo alla fine, se necessario, in un formato distruttivo. La regola (e la logica) vuole, insomma, che l'archiviazione in un formato lossy sia sempre l'anello conclusivo della catena di trasformazioni a cui è sottoposto un file.

 L'efficienza del coefficiente 

A questo punto nasce una domanda scontata: perché mai usare un formato di compressione distruttivo, se esistono sistemi non distruttivi che permettono di comprimere e decomprimere uno stesso file infinite volte, conservando tutte le informazioni in esso contenute?

La risposta è che in molti casi la quantità di spazio che una compressione non distruttiva (lossless) riesce a salvare è di molto inferiore al risparmio di spazio ottenibile per mezzo di una compressione distruttiva (lossy).

L'efficienza della compressione viene calcolata dividendo la grandezza originale del file per la sua grandezza una volta compresso. In inglese questo valore si chiama compression rate o, alla latina, ratio; in italiano possiamo chiamarlo coefficiente o fattore di compressione.

A causa del differente tipo di operazioni svolte sull'immagine, in certi casi è opportuno utilizzare un formato di compressione distruttivo, in altri uno non distruttivo. Tipicamente, le immagini grafiche contenenti disegni a tinte uniformi e contorni netti e ben contrastati - le tavole dei fumetti ad esempio - sono le candidate ideali per compressioni del tipo lossless. Al contrario, le foto - soprattutto quelle contenenti un gran numero di colori differenti e transizioni sfumate tra primo piano e sfondo - richiedono compressioni del tipo lossy se si vuole ottenere un risparmio significativo di spazio.

Ma vediamo, per mezzo di una tabella riassuntiva, i guadagni di spazio che si possono ottenere con ciascuno dei due metodi di compressione dei file grafici.

Tab. 1	Tipi di compressione
COEFFICIENTI DI COMPRESSIONE OTTENIBILI	Non distruttiva (lossless)	Distruttiva (lossy)
Immagini naturali (foto digitali, scansioni)	1:1,5 - 1:2	1:1,5 - 1:30	senza una visibile perdita di qualità
		1:10 - 1:300	con perdita di qualità
Immagini artificiali (disegni, fumetti)	1:1,5 - 1:20	1:1,5 - 1:300

Questa tabella ci dice, quindi, che un file grafico di 1024 x 768 pixel in modalità RGB, che, come abbiamo visto più sopra, occupa in forma non compressa 2.304 Kb, può "dimagrire" con una compressione non distruttiva fino a ridursi, nel migliore dei casi, a poco più di 115 Kb, cioè un ventesimo della grandezza originaria. Questo, però, se l'immagine rappresentata nel file è un disegno, un fumetto. Nel caso sia invece una foto, il meglio che possiamo sperare dalla compressione non distruttiva è un dimezzamento del peso del file: da 2.304 a 1.150 Kb circa.

Ben diversi sono i fattori di compressione che possiamo ottenere ricorrendo all'uso di formati distruttivi. Il file contenente la scansione di una foto può ad esempio essere ridotto fino ad un trentesimo circa della grandezza originaria (cioè meno di 77 Kb sui 2.304 Kb di partenza del nostro esempio) senza alcuna perdita di qualità apparente. Se, poi, non ci infastidisce un certo progressivo, visibile degrado dell'immagine, possiamo ottenere fattori di compressione addirittura del 300 per cento, che porterebbero il nostro file da 2.304 a poco meno di 8 Kb!

Evidente, dunque, la necessità di usare per la visualizzazione su Internet, soggetta alla lentezza delle connessioni via modem, i formati distruttivi, grazie alle loro superiori capacità di compressione.

 L'algoritmo RLE (Run Lenght Encoding) 

Proviamo ora a vedere come funziona un sistema di compressione non distruttivo, tuttora diffuso, noto con la sigla RLE, acronimo di Run Lenght Encoding, che potremmo rendere in italiano con codifica della lunghezza di stringa. In questo tipo di compressione, ogni serie ripetuta di caratteri (o run, in inglese) viene codificata usando solo due byte: il primo è utilizzato come contatore, e serve per memorizzare quanto è lunga la stringa; il secondo contiene invece l'elemento ripetitivo che costituisce la stringa.

Immaginate ora di comprimere in questo formato un file grafico contenente un grande sfondo di un solo colore uniforme. Tutte le volte che l'analisi sequenziale del file s'imbatterà in stringhe di caratteri uguali, e ciò accadrà spesso nella scansione dello sfondo omogeneo, le serie ripetitive potranno essere ridotte a due caratteri soltanto: uno che esprime il numero delle ripetizioni, il secondo il valore che si ripete. E il risparmio di spazio sarà direttamente proporzionale al livello di uniformità presente nell'immagine.

Provate ora, invece, ad usare il sistema RLE su una foto piena di colori differenti e di transizioni sfumate: il risparmio di spazio sarà molto minore, perché poche saranno le stringhe di ripetizioni che l'algoritmo riuscirà a trovare leggendo sequenzialmente il file.

Pensate, infine, al caso limite di un'immagine creata artificialmente, come quella riportata qui sotto, contenente una serie di pixel tutti differenti l'uno dall'altro nei valori cromatici. In questo caso, l'uso della compressione RLE si dimostra addirittura controproducente.

Fig.1 - Immagine ingrandita di un file di 16 x 16 pixel, costituito da 256 colori unici differenti

Questo file, salvato in formato BMP non compresso, occupa 822 byte. Salvato invece sempre in formato BMP, ma utilizzando l'algoritmo RLE, occupa 1400 byte, cioè 1,7 volte la sua grandezza originale.

 L'algoritmo Huffman 

Quest'algoritmo non distruttivo fu inventato nel 1952 dal matematico D.A. Huffman ed è un metodo di compressione particolarmente ingegnoso. Funziona in questo modo:

1. analizza il numero di ricorrenze di ciascun elemento costitutivo del file da comprimere: i singoli caratteri in un file di testo, i pixel in un file grafico.
2. Accomuna i due elementi meno frequenti trovati nel file in una categoria-somma che li rappresenta entrambi. Così ad esempio se A ricorre 8 volte e B 7 volte, viene creata la categoria-somma AB, dotata di 15 ricorrenze. Intanto i componenti A e B ricevono ciascuno un differente marcatore che li identifica come elementi entrati in un'associazione.
3. L'algoritmo identifica i due successivi elementi meno frequenti nel file e li riunisce in una nuova categoria-somma, usando lo stesso procedimento descritto al punto 2. Il gruppo AB può a sua volta entrare in nuove associazioni e costituire, ad esempio, la categoria CAB. Quando ciò accade, la A e la B ricevono un nuovo identificatore di associazione che finisce con l'allungare il codice che identificherà univocamente ciascuna delle due lettere nel file compresso che verrà generato.
4. Si crea per passaggi successivi un albero costituito da una serie di ramificazioni binarie, all'interno del quale appaiono con maggiore frequenza e in combinazioni successive gli elementi più rari all'interno del file, mentre appaiono più raramente gli elementi più frequenti. In base al meccanismo descritto, ciò fa sì che gli elementi rari all'interno del file non compresso siano associati ad un codice identificativo lungo, che si accresce di un elemento ad ogni nuova associazione. Gli elementi invece che si ripetono più spesso nel file originale sono anche i meno presenti nell'albero delle associazioni, sicché il loro codice identificativo sarà il più breve possibile.
5. Viene generato il file compresso, sostituendo a ciascun elemento del file originale il relativo codice prodotto al termine della catena di associazioni basata sulla frequenza di quell'elemento nel documento di partenza.

Il guadagno di spazio al termine della compressione è dovuto al fatto che gli elementi che si ripetono frequentemente sono identificati da un codice breve, che occupa meno spazio di quanto ne occuperebbe la loro codifica normale. Viceversa gli elementi rari nel file originale ricevono nel file compresso una codifica lunga, che può richiedere, per ciascuno di essi, uno spazio anche notevolmente maggiore di quello occupato nel file non compresso.

Dalla somma algebrica dello spazio guadagnato con la codifica breve degli elementi più frequenti e dello spazio perduto con la codifica lunga degli elementi più rari si ottiene il coefficiente di compressione prodotto dall'algoritmo Huffman. Da quanto detto si deduce che questo tipo di compressione è tanto più efficace quanto più ampie sono le differenze di frequenza degli elementi che costituiscono il file originale, mentre scarsi sono i risultati che si ottengono quando la distribuzione degli elementi è uniforme.

Un'ottima dimostrazione del funzionamento di questo algoritmo è visionabile su Internet all'indirizzo http://www.cs.sfu.ca/CC/365/li/squeeze/Huffman.html. Qui troverete un'applet java in grado di eseguire la generazione dell'albero delle associazioni, di produrre il codice compresso e di calcolare il coefficiente finale di compressione. Nelle due immagini sotto riportate, tratte dall'uso di questa applet, potete osservare l'albero generato dalla frequenza di ricorsività delle lettere costituenti un noto scioglilingua ed il risultato della compressione Huffman ottenuta.

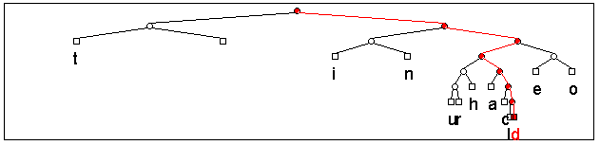
Fig. 2 - L'albero delle associazioni relativo al testo di uno scioglilingua. La struttura dell'albero mostra che le lettere d e  l sono le meno frequenti di tutte

Fig. 3 - La compressione ottenuta ha permesso un risparmio di spazio pari a quasi il 60%

 L'algoritmo LZW (Lempel-Ziv-Welch) 

L'algoritmo non distruttivo che va sotto il nome di LZW è il risultato delle modifiche apportate nel 1984 da Terry Welch ai due algoritmi sviluppati nel 1977 e nel 1978 da Jacob Ziv e Abraham Lempel, e chiamati rispettivamente LZ77 e LZ78.

Il funzionamento di questo metodo è molto semplice: viene creato un dizionario delle stringhe di simboli ricorrenti nel file, costruito in modo tale che ad ogni nuovo termine aggiunto al dizionario sia accoppiata in modo esclusivo un'unica stringa. Esiste un dizionario di partenza costituito dai 256 simboli del codice ASCII, che viene incrementato con l'aggiunta di tutte le stringhe ricorrenti nel file, che siano maggiori di un carattere. Ciò che viene memorizzato nel file compresso è un codice breve che rappresenta in modo inequivocabile la stringa inserita nel dizionario così creato.

Esiste, naturalmente, un insieme di regole non ambigue per la codifica del dizionario, che permetterà in seguito al sistema di decompressione di generare un dizionario esattamente uguale a quello di partenza, in modo tale da poter effettuare l'operazione inversa a quella di compressione, consistente nella sostituzione del codice compresso con la stringa originale. La reversibilità completa e precisa dell'operazione è indispensabile al fine di riottenere l'esatto contenuto del file originale.

Il risparmio di spazio in un file compresso con LZW dipende dal fatto che il numero di bit necessari a codificare il "termine" che rappresenta una stringa nel dizionario è inferiore al numero di bit necessari a scrivere nel file non compresso tutti i caratteri che compongono la stringa. Quanto più numerose e lunghe sono le stringhe che è possibile inserire nel dizionario, tanto maggiore sarà il coefficiente di compressione del file. I formati grafici più noti che utilizzano l'algoritmo LZW sono il TIFF e il GIF. Esso è utilizzato anche dallo standard V.42bis, implementato su tutti i modem di ultima generazione come uno dei protocolli per la trasmissione di dati compressi.

Per avere una dimostrazione pratica di come funziona questo tipo di codifica per mezzo di dizionari di simboli, potete collegarvi su Internet alla pagina http://www.cs.sfu.ca/CC/365/li/squeeze/LZW.html, dalla quale è possibile accedere ad una interessante applet java. La sua interfaccia, molto intuitiva, vi consentirà di effettuare in prima persona una codifica di stringhe di testo con LZW, verificando direttamente la creazione del dizionario, la sua ricostruzione in un'altra finestra ed il coefficiente finale di compressione ottenuto. 

Fig. 4 - Il medesimo dizionario creato in fase di compressione viene generato durante la decompressione del file

 Il formato grafico GIF e la perdita di informazioni sui colori 

La sigla GIF sta per Graphics Interchange Format, un formato grafico sviluppato alla fine degli anni '80 da CompuServe. La compressione operata da GIF usa l'algoritmo LZW, che, come abbiamo visto poco sopra, è un criterio di compressione non distruttivo. Tuttavia salvare un file in formato GIF può comportare una sensibile perdita di informazioni: ciò accade quanto l'immagine di partenza è codificata in uno spazio colore (RGB, CMYK, L*a*b) non riproducibile integralmente per mezzo della tavolozza indicizzata, contenente fino a un massimo di 256 colori, che è lo standard interno del formato GIF.

In un caso simile, la quantità di colori presenti nell'immagine originale viene drasticamente ridotta, ricorrendo ad una serie di algoritmi di trasformazione opportunamente supportati dai più comuni e diffusi programmi di grafica.

L'esito della riduzione sarà un'immagine codificata con un minimo di 1 bit per pixel fino ad un massimo di 8 bit per pixel. La codifica con un solo bit per pixel genera immagini GIF in bianco e nero, dove uno dei due valori possibili del bit (acceso o spento, 1 o 0) rappresenta il nero e l'altro il bianco. Al crescere del numero dei bit adoperati avremo formati GIF con 4, 8, 16, 32, 64, 128 o 256 colori, valore, quest'ultimo, corrispondente all'uso di 8 bit per pixel.

Data un'immagine a colori in modalità RGB, avente una profondità del colore di 24 bit, la conversione ad una tavolozza a 256 colori porterà ad una riduzione di un terzo della grandezza del file (24 bit / 8 bit = 3). Ciò prima ancora che sia applicata la compressione basata sull'algoritmo LZW. Riduzioni di grandezza proporzionalmente maggiori si ottengono se la tavolozza usata per la conversione contiene 128, 64, 32, 16, 8, 4 o solo 2 colori.

La conversione operata sull'immagine originale trasforma i valori RGB di ciascun pixel in un valore RGB approssimato, dipendente dal tipo di tavolozza-colore prescelto per effettuare l'operazione. I valori cromatici di questa tavolozza saranno poi inglobati nel file GIF generato, in modo da consentire, in fase di decompressione, di generare a monitor un'immagine corrispondente ai valori salvati. Tra le varie opzioni di conversione del colore che i più diffusi programmi di grafica mettono a disposizione dell'utente, citiamo le seguenti tavolozze:

• adattata - cerca di mantenere i colori del file compresso quanto più possibile simili a quelli del file originale;
• ottimizzata - codifica i 256 colori sulla base della loro presenza percentuale all'interno dell'immagine originale;
• uniforme - contiene uguali proporzioni di rosso, di verde e di blu;
• di sistema - fornisce i colori predefiniti del sistema operativo Microsoft Windows;
• Internet Explorer - fornisce i colori predefiniti usati dal browser della Microsoft;
• Netscape Navigator - fornisce i colori standard utilizzati dal browser della Netscape;
• personalizzata - consente di aggiungere colori a scelta dell'utente fino a completare la gamma dei 256 possibili.

E' chiaro, però, che, qualsiasi sia la tavolozza adoperata, l'immagine ricostruita a partire dai dati salvati nel file GIF non sarà uguale all'immagine RGB originale e sarà tanto più "povera" d'informazione quanto maggiore sarà il numero dei colori presenti nell'immagine di partenza che vengono eliminati per approssimazione, in modo da avere alla fine una tavolozza di 256 colori al massimo.

Delle tre foto qui sotto riportate, quella a sinistra è l'immagine originale, che contiene ben 49.131 colori unici. Quella centrale è una GIF basata su una tavolozza di 256 colori uniformi: mostra delle evidenti bande di transizione, che denotano la natura distruttiva della riduzione del colore operata; l'immagine a destra è anch'essa una GIF a 256 colori, che usa però una tavolozza adattata, in grado di preservare un alto grado di corrispondenza visiva all'originale. Il limite d'uso di questo tipo di tavolozza è nell'impredicibilità della riproduzione dell'immagine su computer differenti, la cui dotazione hardware e software si discosti da quella del computer su cui è stato generato il file GIF. 

Fig. 5 - La foto centrale e quella a destra sono due GIF derivate dall'immagine originale di sinistra, la prima con una tavolozza uniforme, la seconda con una tavolozza adattata

 Drastiche riduzioni di peso con lo standard JPEG 

La sigla JPEG identifica una commissione di esperti denominata Joint Photographic Expert Group, formata nel 1986 con lo scopo di stabilire uno standard di compressione per le immagini a tono continuo - cioè di tipo fotografico - sia a colori sia in bianco e nero. Il lavoro di questa commissione ha portato alla definizione di una complessa serie di algoritmi, approvata come standard ISO nell'agosto del 1990 e successivamente divenuta la raccomandazione T.81 (9/92) dell'ITU, International Telecommunication Union. Chi la sera a letto ha difficoltà ad addormentarsi, può leggerne la versione integrale, scaricabile in formato PDF dal sito del W3C. L'indirizzo è http://www.w3.org/Graphics/JPEG/itu-t81.pdf: sono 186 pagine fitte di definizioni, procedure, grafici, immagini esemplificative e formule matematiche. Auguri di buona lettura!

Il JPEG è dunque uno standard industriale e non va confuso con il formato di file JPG, che rappresenta di volta in volta, a seconda della software house che lo implementa, un sottoinsieme variabile e non sempre universalmente compatibile dello standard di riferimento. Pochi ad esempio sanno che le specifiche JPEG descrivono anche un formato di compressione non distruttivo, basato su tecniche differenti da quelle che descriveremo qui di seguito, del quale si è ormai persa traccia, non usando gli sviluppatori di programmi di grafica - a causa delle sue non straordinarie prestazioni - inserirlo tra le varie opzioni di salvataggio dei normali file JPG.

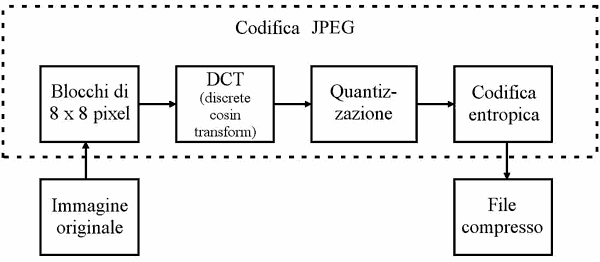
Fig. 6 - Schematizzazione semplificata del processo di compressione JPEG

Ecco in dettaglio la sequenza di operazioni che da un'immagine originale non compressa porta ad un'immagine compressa con JPEG.

1) Trasformazione dello spazio colore - A causa delle particolari caratteristiche dell'occhio umano, molto più sensibile alle variazioni di luminosità che alle variazioni cromatiche, è opportuno innanzitutto trasformare la modalità RGB in modalità YUV. E' questo lo spazio-colore definito per il sistema televisivo PAL. Tra i suoi equivalenti nel campo della computergrafica c'è il metodo L*a*b presente in Adobe Photoshop.

Il sistema YUV scompone l'informazione relativa a ciascun pixel in due componenti: la luminanza, che definisce il grado di luminosità nella scala da nero a bianco (la lettera Y della sigla YUV), e la crominanza, che definisce il colore in base al rapporto tra due assi, uno che va da blu a giallo (la lettera U) e l'altro che va da rosso a verde (la lettera V).

Eseguire la trasformazione dallo spazio-colore RGB allo spazio-colore YUV non è indispensabile, ma il farlo consente di ottenere una maggiore compressione JPEG. Quando, infatti, le successive trasformazioni matematiche che si applicano all'immagine trovano l'informazione nettamente suddivisa nelle due componenti di luminosità e di colore, possono procedere all'eliminazione di molte informazioni relative al colore senza intaccare quelle relative alla luminosità, più importanti per la visione umana, e senza causare, in tal modo, danni visibili al contenuto dell'immagine. Ciò non è possibile invece nella stessa misura quando gli algoritmi di compressione si applicano a valori RGB, che presentano l'informazione relativa al colore e quella relativa alla luminosità fuse insieme (per le immagini in scala di grigio la conversione non ha senso, in quanto l'informazione sulla luminosità è già disponibile in partenza).

2) Riduzione, in base alla componente, di gruppi di pixel a valori medi - E' un'operazione opzionale, di cui alcuni software di grafica consentono l'impostazione. La componente che esprime la luminanza è lasciata invariata, mentre la componente cromatica viene dimezzata in orizzontale e in verticale, oppure soltanto in orizzontale. Ciò si esprime con il rapporto 2:1 per indicare il dimezzamento e con il rapporto 1:1 per indicare che la componente è lasciata invariata. Alcuni programmi di grafica, tra le opzioni di salvataggio in JPG, mostrano stringhe esoteriche come 4-1-1 e 4-2-2, che esprimono appunto il coefficiente di riduzione che viene applicato alle componenti cromatiche dell'immagine. Tale operazione, che fa parte degli algoritmi distruttivi dello standard JPEG, riduce in partenza il file di una metà o di un terzo della sua grandezza originale. Non si applica alle immagini a toni di grigio e ciò spiega perché queste siano meno comprimibili in generale delle immagini a colori.

3) DCT applicata a blocchi di 8 x 8 pixel suddivisi in base alla componente - La sigla DCT sta per Discrete Cosine Transform: si tratta di una serie di operazioni matematiche che trasformano i valori di luminosità e colore di ciascuno dei 64 pixel di ogni blocco preso in esame in altrettanti valori di frequenza. In particolare, mentre i valori dei pixel contenuti nei blocchi di 8 x 8 tratti dall'immagine originale variano da 0 a 255, dopo l'esecuzione della DCT essi, trasformati in frequenze, variano da -721 a 721. Dov'è allora il guadagno? In una sottile combinazione di quantizzazione e codifica entropica. In termini più semplici, la trasformazione dei valori in frequenze consentirà nei passaggi successivi di tagliare più informazioni senza apparente perdita visiva di quante se ne potrebbero tagliare lavorando sui valori naturali dei pixel. Inoltre la sequenza a zig zag in cui i nuovi valori vengono scritti consente di applicare ad essi una compressione (Huffman o aritmetica) più efficace.

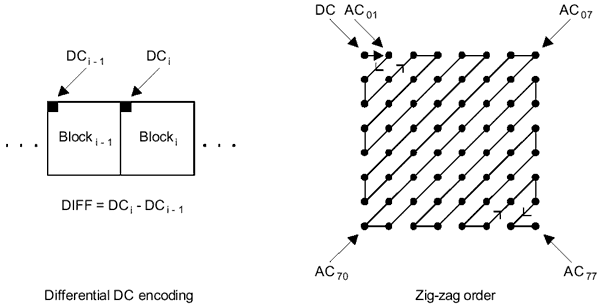
Fig. 7 - Scrittura a zig zag dei valori ottenuti con la DCT, a partire dall'angolo superiore sinistro del blocco di 8 x 8 pixel (schemi tratti dalle specifiche ufficiali JPEG ITU.T81)

4) Divisione e arrotondamento all'intero dei 64 valori ottenuti con la DCT - Ciascuno dei 64 valori di frequenza viene diviso per uno specifico coefficiente di quantizzazione, codificato in apposite tavole di riferimento. Il risultato della divisione viene arrotondato all'intero più vicino. L'eliminazione dei decimali è la principale operazione di compressione distruttiva dello standard JPEG. Il tutto è studiato in modo che le frequenze più importanti per l'occhio umano, cioè le più basse, memorizzate nell'angolo superiore sinistro del blocco di 8 x 8, siano preservate, mentre le più alte, la cui perdita è relativamente ininfluente, vengano eliminate.

5) Compressione non distruttiva dei coefficienti quantizzati - Ai valori risultanti dalla divisione e dall'arrotondamento sopra descritti viene applicata una compressione non distruttiva, per la quale può essere utilizzato l'algoritmo Huffman o una codifica aritmetica chiamata Q-coding. Quest'ultima è di circa il 5-10 % più efficace della Huffman, ma è protetta da brevetto, per cui il suo uso non è gratuito. Per tale motivo i software che realizzano la compressione JPG implementano solo l'algoritmo Huffman.

6) Inserimento nel file compresso di intestazioni e parametri per la decompressione - Affinché il file possa essere in seguito decompresso e possa generare un'immagine il più possibile somigliante all'originale non compresso, occorre che nel file JPG siano inserite le tabelle contenenti i coefficienti di quantizzazione e i valori di trasformazione della codifica Huffman.

Due precisazioni in conclusione di paragrafo. La prima riguarda il noto fenomeno dei blocchi quadrettati, che sono spesso chiaramente visibili nelle immagini JPG molto compresse e rappresentano un forte elemento di degrado della qualità. Essi sono la conseguenza diretta dell'algoritmo che suddivide l'immagine di partenza in blocchi da 8 x 8 pixel. Le varie trasformazioni applicate ai valori dei pixel di ciascun blocco sono del tutto indipendenti dalle trasformazioni applicate ai pixel dei blocchi adiacenti. Ciò causa talvolta transizioni brusche tra pixel adiacenti appartenenti a blocchi differenti. Il fenomeno è tanto più appariscente quanto più l'immagine contiene aree di colore uniforme e linee sottili ben separate dallo sfondo.

Fig. 8 - A destra un particolare molto ingrandito della foto di sinistra, che mostra in modo inequivocabile la quadrettatura tipica risultante dalla compressione JPEG

La seconda precisazione riguarda il significato dell'espressione codifica entropica, utilizzata al precedente punto 3). Questa locuzione traduce l'inglese entropy coding (o encoding) ed esprime un tipo di compressione non distruttiva - quale ad esempio l'algoritmo Huffman - che, data una serie qualsiasi di simboli, è in grado di codificarli utilizzando il minor numero possibile di bit.

 JPEG 2000, l'evoluzione della specie... 

Il successo dello standard di compressione JPEG si può desumere dalle cifre: è stato calcolato infatti che l'80 % circa delle immagini presenti su Internet siano file JPG. Tuttavia esiste già il successore designato di questo fortunato standard: si tratta di un algoritmo che va sotto il nome di JPEG 2000 e che si prevede sarà ufficializzato come standard ISO / ITU entro l'anno 2001. I soliti insonni che volessero leggersi la versione completa delle specifiche relative a questo formato possono scaricarla a partire dalla pagina http://www.jpeg.org/FCD15444-1.htm.

Ma come funziona precisamente JPEG 2000? Quali sono le principali differenze rispetto al fratello maggiore JPEG?

Le differenze sono numerose e la principale è senz'altro il cambiamento dello strumento matematico alla base dell'algoritmo di compressione. Mentre, infatti, JPEG usa la trasformata chiamata DCT (Discrete Cosine Transform, vedi sopra), JPEG 2000 usa la cosiddetta DWT, Discrete Wavelet Transform.

La parola wavelet, "piccola onda" in italiano, identifica un sistema matematico che consente di superare il difetto principale delle immagini trattate secondo il normale standard JPEG, cioè la presenza di quei blocchi quadrettati che sono il prezzo da pagare per la maggior compressione ottenuta.

Con l'uso della DWT, il contenuto del file originale non viene più suddiviso in blocchi da 8 x 8 pixel, ma è l'immagine nella sua totalità ad essere analizzata e successivamente scomposta, per ottenere alla fine un file compresso dove l'eventuale degrado dell'immagine è significativamente inferiore a quello ottenibile, a parità di compressione, con il JPEG tradizionale: un degrado che si manifesta non più attraverso i famosi blocchi quadrettati, ma con un aspetto più o meno sfocato dei contorni degli oggetti presenti nell'immagine.

Ma vediamo in dettaglio quali sono le fasi della compressione eseguita con l'algoritmo JPEG 2000.

1) Preparazione dell'immagine - La trasformazione wavelet agisce decorrelando i contenuti a bassa frequenza - più importanti per la visione umana - dai contenuti ad alta frequenza. Per far ciò è necessario che l'immagine originale sia suddivisa in quattro immagini più piccole, dotate ciascuna di un numero di colonne e di righe uguale ad esattamente la metà del file iniziale. La preparazione consiste dunque nel fornire alla DWT una griglia di righe e colonne tale da consentire la ripetizione dell'operazione di suddivisione in quattro ad ogni successivo stadio del ciclo di trasformazione operato con la DWT.

2) Trasformazione - L'immagine viene trasformata dalla DWT e poi scalata, in modo da ottenere quattro immagini alte e larghe ciascuna esattamente la metà dell'originale. Nel quadrante superiore sinistro, grazie all'uso di un filtro passa-basso, sono salvate le basse frequenze presenti nel file di partenza. Negli altri tre quadranti, grazie all'uso di un filtro passa-alto, sono salvate le alte frequenze. Il risultato di quest'operazione è la decorrelazione tra le informazioni di bassa e alta frequenza contenute nell'immagine.

Il passaggio successivo consiste nella ripetizione del medesimo procedimento, applicato stavolta solo all'immagine del quadrante superiore sinistro, contenente le basse frequenze. Il risultato del secondo passaggio è rappresentato in fig. 9: l'immagine con le basse frequenze ha ormai altezza e larghezza pari a un quarto dell'originale, mentre tutto il resto è occupato dalle alte frequenze. Il procedimento poi continua per analisi e scalature successive, fino al limite minimo di un'immagine ridotta ad un solo pixel.

Il risultato finale di tutta l'operazione è che l'intero contenuto informativo dell'immagine originale è stato segmentato in una serie di trasformazioni successive, che potranno poi essere compresse in un minimo spazio ed utilizzate in modo reversibile in fase di decompressione, per generare un'immagine il più possibile simile all'originale non compresso.

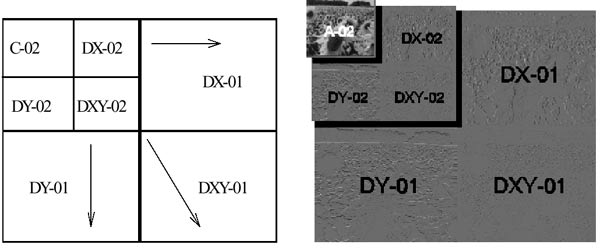
Fig. 9 - Applicazione progressiva della DWT su un'immagine compressa con JPEG 2000

3) Quantizzazione e codifica - La quantizzazione è un'operazione in genere "distruttiva" (lossy), che divide per specifici coefficienti i valori trovati dalla DWT e arrotonda poi i risultati all'intero più vicino. Le fasi di quantizzazione e di codifica hanno lo scopo di selezionare per cicli successivi i dati da comprimere e disporli poi in un ordine preciso all'interno del flusso dei dati. Possono essere implementate come stadi separati, così come avviene nel JPEG standard, con la fase di quantizzazione che elimina la parte meno rilevante dell'informazione e passa il resto all'encoder per la fase di codifica. Ma combinando quantizzazione e codifica in un singolo stadio si ottiene la possibilità di controllare esattamente l'entità della compressione (qualità dell'immagine contro coefficiente di compressione). La dimensione del flusso di dati compresso può essere predefinita con esattezza. In questo caso la quantizzazione dei coefficienti trasformati ha luogo durante la fase di codifica.

Il primo ciclo di quantizzazione ha per così dire una "grana grossa", nel senso che solo i coefficienti maggiori sono presi in considerazione e codificati. Al ciclo successivo gli intervalli di quantizzazione vengono dimezzati, sicché divengono significativi coefficienti più piccoli. Ciò significa che i valori dei coefficienti selezionati nel primo ciclo sono specificati in modo sempre più preciso dalle informazioni aggiunte ad ogni successivo ciclo di quantizzazione e codifica. I cicli continuano finché il flusso dei dati non ha raggiunto la sua lunghezza predefinita oppure finché tutta l'informazione presente nell'immagine non viene codificata. Questo modo di incorporare nella sequenza finale di dati strutture via via più raffinate consente di ricostruire l'immagine iniziale a partire da qualsiasi blocco di dati contenuto nel file compresso, con la limitazione che la qualità dell'immagine ricostruita sarà tanto migliore quanto minore sarà la parte di dati non utilizzata dell'intero flusso.

Una simile caratteristica è importantissima per i futuri usi di questo formato su Internet. I file compressi con JPEG 2000 racchiudono infatti al loro interno più risoluzioni differenti della stessa immagine. I produttori di software potranno implementare perciò dei comandi in grado di consentire all'utente collegato via Internet di decidere, in base al tempo stimato per il download, quale risoluzione dell'immagine visualizzare nel proprio browser. I file JP2 (è questa l'estensione proposta per identificare lo standard JPEG 2000) consentiranno insomma di racchiudere in un unico documento l'anteprima - il cosiddetto thumbnail - la bassa, la media e l'alta risoluzione di una stessa immagine, senza però moltiplicare proporzionalmente il peso del file.

Ecco per concludere un elenco delle principali, innovative caratteristiche previste dalle specifiche JPEG 2000:

1. supporto per differenti modalità e spazi-colore (immagini a due toni, in scala di grigi, a 256 colori, a milioni di colori, in standard RGB, PhotoYCC, CIELAB, CMYK);
2. supporto per differenti schemi di compressione, adattabili in base alle esigenze;
3. standard aperto a successive implementazioni legate al sorgere di nuove necessità;
4. supporto per l'inclusione di un'illimitata quantità di metadati nello spazio di intestazione del file, utilizzabili per fornire informazioni private o per interagire con applicazioni software (guidare, ad esempio, il browser allo scaricamento di appositi plug-in da Internet);
5. stato dell'arte per la compressione distruttiva e non distruttiva delle immagini, con un risparmio di spazio a parità di qualità, rispetto allo standard JPEG, dell'ordine del 20-30 %;
6. supporto per immagini più grandi di 64k x 64k pixel, ovvero maggiori di 4 Gb;
7. singola architettura per la decompressione dei file, in luogo dei 44 modi codificati per il vecchio JPEG, molti dei quali legati a specifiche applicazioni e non utilizzati dalla maggior parte dei decompressori;
8. supporto per la trasmissione dei dati in ambienti disturbati, per esempio attraverso la radiotelefonia mobile;
9. capacità di maneggiare indifferentemente sia le immagini naturali sia la grafica generata al computer;
10. supporto per la codifica di ROI (Region Of Interest), cioè di zone ritenute più importanti e perciò salvate con una risoluzione maggiore di quella usata per il resto dell'immagine.

Abbiamo detto che JPEG 2000 non è ancora uno standard a tutti gli effetti. Ma come fare per vedere in anteprima i risultati della compressione wavelet? Semplice! Basta scaricare LuraWave, un programma sviluppato da LuraTech (http://www.luratech.com), società specializzata nella ricerca e produzione di software per la compressione dei dati. Con LuraWave è possibile salvare immagini in LWF, un formato che usa appunto le tecniche di compressione qui sopra descritte. Nella Fig.10 qui sotto riportata, si può vedere la differenza tra due immagini fortemente compresse, l'una con LuraWave l'altra con il normale JPEG, differenza che appare a tutto vantaggio della compressione di tipo wavelet.

Fig. 10 - L'immagine prodotta con LuraWave (1:150 rispetto all'originale) mostra, a paragone con JPEG e a parità di peso, un degrado molto minore rispetto all'originale

 Tutto gratis e senza perdite? Ecco allora il formato PNG 

PNG (pronunciato ping) è l'acronimo di Portable Network Graphics. Per i sostenitori di questo formato, però, la sigla PNG significa PNG's Not GIF, cioè PNG non è GIF, volendo intendere con questa precisazione che PNG è molto meglio di GIF.

La questione nasce con l'annuncio fatto nel 1995 da CompuServe e Unisys: da quel momento in poi, l'implementazione del formato GIF in prodotti software avrebbe comportato il pagamento di una quota-diritti ad Unisys, quale legale detentore del brevetto sull'algoritmo di compressione LZW, usato all'interno del formato GIF.

PNG nasce quindi in contrapposizione a GIF, come un formato grafico compresso e allo stesso tempo del tutto gratuito, anche se per la verità va precisato che il suo sviluppo è stato portato avanti in modo indipendente e avendo di mira risultati di più ampia portata che la semplice fuga dal pagamento dei diritti dovuti ad Unisys.

Ma quali sono le principali caratteristiche di PNG? L'elenco seguente ci mostra fino a che punto questo formato possa essere assimilato per alcune caratteristiche a GIF, ma di quanto poi se ne discosti, sopravanzandolo alla fine in prestazioni e versatilità.

1) Compressione - PNG punta tutto sulla compressione non distruttiva. Non esistono opzioni per salvare un file PNG in modo non compresso né opzioni per salvarlo con una compressione distruttiva. Però l'algoritmo non distruttivo alla base di PNG è davvero potente. I risultati che si ottengono sono in genere del 20% migliori di quelli ottenibili con la compressione GIF. Lo strumento di compressione, gratuitamente utilizzabile da chiunque, è zlib - una variante dell'algoritmo LZ77 -, sviluppato per la parte di compressione da Jean-loup Gailly (http://gailly.net/) e per quella di decompressione da Mark Adler (http://www.alumni.caltech.edu/~madler/), ed attualmente giunto alla versione 1.1.3.

In più la capacità di compressione del PNG può in certi casi essere di molto aumentata grazie all'adozione di particolari filtri: si tratta di sistemi di trasformazione dell'ordine dei dati che costituiscono l'immagine, studiati per esaltare il coefficiente di compressione raggiungibile. Addirittura vi è il caso limite di un'immagine che, non compressa, occupa 48 Mb, compressa con PNG ma non filtrata occupa 36 Mb, filtrata, infine, si riduce - incredibile ma vero! - a soli 115.989 byte. Il filtro, in questo caso, migliora di ben 300 volte la capacità del motore di compressione incorporato in PNG! Il file in questione è un'immagine RGB di 512 x 32.768 pixel che mostra in sequenza tutti i 16.777.216 colori codificabili con 24 bit per pixel. Chi volesse testare direttamente questo file molto particolare, può farlo collegandosi a http://www.libpng.org/pub/png/img_png/16million.png.

2) Controllo di errore - PNG dispone di un sistema chiamato CRC-32, ovvero cyclic redundancy check ("controllo di ridondanza ciclico") a 32 bit, che associa valori di controllo ad ogni blocco di dati ed è in grado di rilevare immediatamente qualsiasi corruzione delle informazioni salvate o trasmesse via Internet.

3) Supporto per milioni di colori - Le immagini PNG non sono limitate ad un massimo di 256 colori come accade per i file GIF, ma supportano anche la modalità RGB. Non supportano per ora la modalità CMYK, anche se si prevede la possibilità di una futura estensione che ne consenta il trattamento.

4) Canali alfa - Mentre GIF supporta una trasparenza del tipo "tutto o niente" (pixel completamente trasparente o del tutto opaco), PNG permette, grazie all'uso dei cosiddetti canali alfa, la possibilità di una trasparenza variabile su 254 livelli di opacità. Questa caratteristica favorisce, ad esempio, la creazione del classico effetto di ombre cadute, ombre che si conservano indipendentemente dal colore dello sfondo su cui vengono visualizzate.

5) Interlacciamento - In caso di connessioni via modem particolarmente lente, può essere molto utile cominciare a vedere fin da subito un'anteprima, sia pure poco definita, dell'immagine che si sta scaricando. Con la funzione di interlacciamento di cui è dotato il formato PNG ciò è possibile molto più velocemente che con l'analoga funzione incorporata nel formato GIF. Per quanto riguarda GIF, l'interlacciamento - cioè la visualizzazione parziale e progressiva dell'immagine - è monodimensionale e la prima apparizione di contenuti visibili richiede l'invio di un ottavo dei dati-immagine complessivi. L'interlacciamento di PNG è invece bidimensionale e basta l'invio di solo un sessantaquattresimo dei dati per avere la prima visualizzazione grossolana dell'immagine.

6) Correzione di gamma - Il formato PNG integra un sistema di correzione di gamma, che permette di compensare, sia pure solo approssimativamente, le differenze di visualizzazione di un'immagine nel passaggio da una piattaforma hardware ad un'altra.

Ma c'è, infine, almeno una caratteristica in cui GIF sia preferibile senza dubbio a PNG? Sì, c'è, ed è il supporto per le immagini animate. In un file GIF, come ben sa la maggior parte di coloro che navigano in Internet, è possibile racchiudere una sequenza di immagini che, fatte scorrere in rapida successione, danno l'impressione del movimento. Questo effetto non è disponibile nel formato PNG, pensato e sviluppato per il solo trattamento delle immagini statiche.

Ed in conclusione un piccolo esperimento, fatto per verificare direttamente il coefficiente medio di compressione ottenibile con PNG a paragone di quello ottenibile con un altro formato non distruttivo: il TIFF con compressione LZW. La banconota da 10 euro - qui sotto raffigurata in un esemplare JPG delle medesime dimensioni in pixel utilizzate per la prova descritta - è salvata in un file TIFF di 431 x 244 pixel, non compresso, che pesa esattamente 308,8 Kb. Compresso con l'algoritmo LZW di TIFF, il file si riduce a 226,3 Kb, con un risparmio di spazio del 27% rispetto all'originale (coefficiente di compressione = 1:1,364). Lo stesso file, salvato come PNG, si riduce a 177,9 Kb. Il risparmio di spazio rispetto all'originale sale al 42,4% (coefficiente di compressione = 1:1,735). Nel caso specifico, il salvataggio del file in formato PNG ha prodotto un risparmio di spazio di quasi il 22% rispetto al salvataggio in formato TIFF compresso con LZW.

Fig. 11 - Il retro di una banconota da 10 euro. L'immagine, salvata come PNG, ottiene un coefficiente di compressione migliore di circa il 22% rispetto alla compressione LZW di TIFF (in questo esempio l'immagine è una normale JPG)

 In conclusione 

Siamo arrivati per ora alla fine di questo viaggio a volo d'angelo nel mondo ricco e variegato degli algoritmi di compressione utilizzati nel mondo delle immagini digitali. Va ribadito, appunto, che il soggetto di queste schede non sono stati i formati grafici in se stessi, ma i motori di compressione che essi adottano. Perciò molti sono stati i formati di file non considerati o citati solo di sfuggita, in riferimento ai sistemi di compressione da essi utilizzati.

Rimandiamo ad un prossimo articolo il completamento di questa panoramica sui sistemi di compressione ed un approfondimento sui formati di file, non solo grafici, in cui essi sono incorporati.