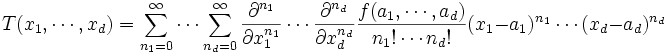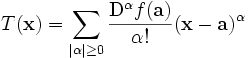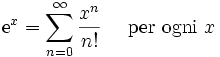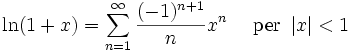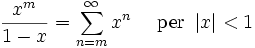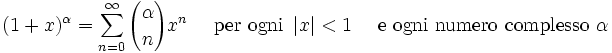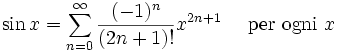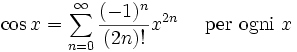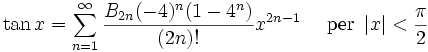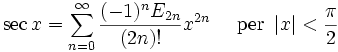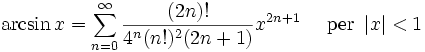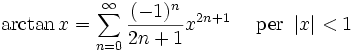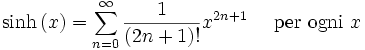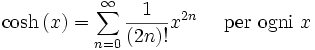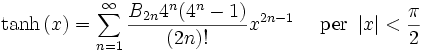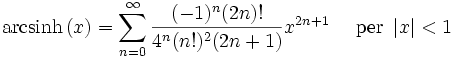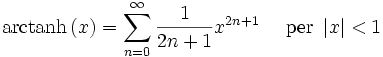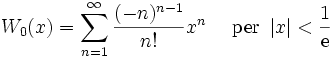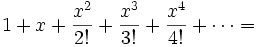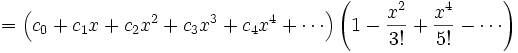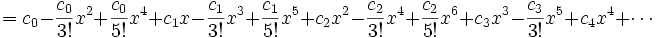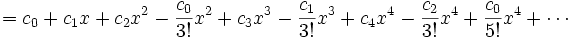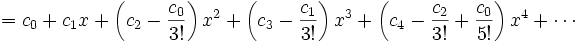Un grande ringraziamento a tutti coloro che hanno donato durante questa raccolta fondi!
Un appello personale del fondatore di Wikipedia Jimmy Wales

Serie di Taylor

Da Wikipedia, l'enciclopedia libera.

Vai a: Navigazione, cerca

Teoria degli insiemi

Funzioni elementari

L'operazione di limite

Serie numeriche

Calcolo differenziale

Integrale indefinito

Immagine:Sintay.png

In matematica, la serie di Taylor di una funzione f definita in un intervallo aperto (a − r, a + r) a valori reali (o complessi) e infinite volte derivabile è la serie di potenze

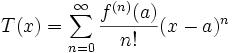$T(x) = \sum_{n=0}^{\infin} \frac{f^{(n)}(a)}{n!} (x-a)^{n}$ .

Qui n! denota il fattoriale di n ed f ⁽ⁿ⁾(a) denota la n-esima derivata della f valutata nel punto a. Se a = 0, la serie viene chiamata anche serie di Maclaurin.

Indice

[nascondi]

1 Cenni storici
2 Proprietà
3 Serie di Taylor in più variabili
4 Sviluppi in serie di Taylor di funzioni di uso comune
5 Calcoli delle serie di Taylor
6 Voci correlate
7 Collegamenti esterni

[modifica]

Cenni storici

La serie di Taylor prende il nome dal matematico inglese Brook Taylor che ha pubblicato le formule sulle serie di potenze nel 1715. Tuttavia James Gregory aveva lavorato con queste serie molto prima di Taylor e aveva pubblicato varie serie di Maclaurin quando Taylor era ancora un ragazzino. Taylor non era a conoscenza del precedente lavoro di Gregory.

Queste serie di potenze in realtà erano state inventate circa tre secoli prima dal matematico indiano Madhava di Sangamagramma; il suo lavoro, come gli altri risultati della cosiddetta scuola matematica del Kerala, era del tutto sconosciuto nell'Europa del XVIII secolo.

[modifica]

Proprietà

Se la serie di Taylor della funzione f(x) converge per ogni x nell'intervallo (a − r, a + r) e se la sua somma è uguale alla f(x), questa funzione viene detta funzione analitica. Per verificare se la serie converge verso f(x), normalmente si usa effettuare stime del termine resto che compare nel teorema di Taylor. Una funzione è analitica se e solo se può essere rappresentata da una serie di potenze; i coefficienti di una tale serie di potenze coincidono necessariamente con quelli che compaiono nella precedente formula per la serie di Taylor.

L'importanza della serie di potenze di Taylor è almeno quadruplice. Innanzi tutto la differenziazione e l'integrazione delle serie di potenze possono essere effettuate termine a termine ed è tendenzialmente piuttosto facile. Secondariamente una funzione analitica può essere estesa univocamente ad una funzione olomorfa definita su un disco aperto nel piano complesso e questa possibilità rende disponibile l'intero meccanismo dell'analisi complessa. In terzo luogo si può utilizzare la serie (troncandola) per valutazioni approssimate della funzione (spesso si procede ad esprimere un polinomio nella forma di Chebyshev e a valutare questo con l'algoritmo di Clenshaw). Quarto motivo, spesso le operazioni algebriche sulle funzioni possono essere effettuate più rapidamente sulle loro rapprsentazioni mediante serie di potenze; ad esempio la dimostrazione più semplice della formula di Eulero si ottiene dagli sviluppi in serie di Taylor per le funzioni esponenziale, seno e coseno. Questo risultato sta a fondamento dell'analisi armonica.

Immagine:Expinvsq.png

Va osservato che si trovano esempi di funzioni infinite volte differenziabili f(x) la cui serie di Taylor converge, ma che non è uguale alla f(x). Consideriamo, ad esempio, la funzione definita a pezzi chiedendo che sia f(x) := exp(−1/x²) per x ≠ 0 ed f(0) := 0; tutte le sue derivate sono nulle per x = 0; quindi la sua serie di Taylor è la serie zero e il suo raggio di convergenza è infinito, anche se la funzione è ben diversa dalla funzione nulla. Questa particolare situazione patologica non affligge le funzioni di una variabile complessa a valori complessi. In effetti la funzione derivata della exp(−1/z²) non tende a zero quando z si avvicina a 0 sevondo l'asse immaginario e quindi la funzione non è olomorfa nell'origine.

Alcune funzioni non possono essere rappresentate mediante serie di Taylor in quanto posseggono una determinata singolarità; in questi casi spesso si riesce ancora a disporre di uno sviluppo in serie facendo uso anche di potenze negative della variabile x; vedi serie di Laurent. Questo ad esempio è possibile per la funzione f(x) = exp(−1/x²).

Un recente avanzamento nei metodi per la determinazione delle serie di Taylor che sono soluzioni di equazioni differenziali è costituito dal teorema di Parker-Sochacki. Questo teorema è un allargamento della iterazione di Picard.

[modifica]

Serie di Taylor in più variabili

Uno sviluppo di Taylor che può considerarsi una generalizzazione del precedente si può applicare anche a funzioni di più di una variabile reale o complessa

$T(x_1,\cdots,x_d) = \sum_{n_1=0}^{\infin} \cdots \sum_{n_d=0}^{\infin} \frac{\partial^{n_1}}{\partial x_1^{n_1}} \cdots \frac{\partial^{n_d}}{\partial x_d^{n_d}} \frac{f(a_1,\cdots,a_d)}{n_1!\cdots n_d!} (x_1-a_1)^{n_1}\cdots (x_d-a_d)^{n_d}$

Lo sviluppo di Taylor troncato al secondo ordine per una funzione a valori scalari in più di una variabile si può scrivere nella seguente forma compatta :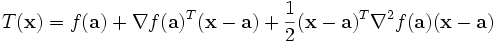 $T(\mathbf{x}) = f(\mathbf{a}) + \nabla f(\mathbf{a})^T (\mathbf{x} - \mathbf{a}) + \frac{1}{2} (\mathbf{x} - \mathbf{a})^T \nabla^2 f(\mathbf{a}) (\mathbf{x} - \mathbf{a})$ ,

dove 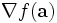$\nabla f(\mathbf{a})$ denota il gradiente della funzione e 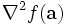$\nabla^2 f(\mathbf{a})$ la sua matrice hessiana. Servendosi della notazione del multi-indice la serie di Taylor per più variabili si scrive

$T(\mathbf{x}) = \sum_{|\alpha| \ge 0}^{}{\frac{\mathrm{D}^{\alpha}f(\mathbf{a})}{\alpha !}(\mathbf{x}-\mathbf{a})^{\alpha}}$

in completa analogia con il caso della singola variabile.

[modifica]

Sviluppi in serie di Taylor di funzioni di uso comune

Presentiamo ora alcuni importanti sviluppi in serie di Taylor. Tutti questi sviluppi sono validi anche per argomenti x complessi.

Funzione esponenziale e logaritmo naturale:

$\mathrm{e}^{x} = \sum^{\infin}_{n=0} \frac{x^n}{n!}\quad\mbox{ per ogni } x$

$\ln(1+x) = \sum^{\infin}_{n=1} \frac{(-1)^{n+1}}n x^n\quad\mbox{ per } \left| x \right| < 1$

Serie geometrica:

$\frac{x^m}{1-x} = \sum^{\infin}_{n=m} x^n\quad\mbox{ per } \left| x \right| < 1$

Sviluppo binomiale:

$(1+x)^\alpha = \sum^{\infin}_{n=0} {\alpha \choose n} x^n\quad\mbox{ per ogni } \left| x \right| < 1\quad\mbox{ e ogni numero complesso } \alpha$

Funzioni trigonometriche:

$\sin x = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n+1)!} x^{2n+1}\quad\mbox{ per ogni } x$

$\cos x = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n)!} x^{2n}\quad\mbox{ per ogni } x$

$\tan x = \sum^{\infin}_{n=1} \frac{B_{2n} (-4)^n (1-4^n)}{(2n)!} x^{2n-1}\quad\mbox{ per } \left| x \right| < \frac{\pi}{2}$

$\sec x = \sum^{\infin}_{n=0} \frac{(-1)^n E_{2n}}{(2n)!} x^{2n}\quad\mbox{ per } \left| x \right| < \frac{\pi}{2}$

$\arcsin x = \sum^{\infin}_{n=0} \frac{(2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1}\quad\mbox{ per } \left| x \right| < 1$

$\arctan x = \sum^{\infin}_{n=0} \frac{(-1)^n}{2n+1} x^{2n+1}\quad\mbox{ per } \left| x \right| < 1$

Funzioni iperboliche:

$\sinh \left(x\right) = \sum^{\infin}_{n=0} \frac{1}{(2n+1)!} x^{2n+1}\quad\mbox{ per ogni } x$

$\cosh \left(x\right) = \sum^{\infin}_{n=0} \frac{1}{(2n)!} x^{2n}\quad\mbox{ per ogni } x$

$\tanh\left(x\right) = \sum^{\infin}_{n=1} \frac{B_{2n} 4^n (4^n-1)}{(2n)!} x^{2n-1}\quad\mbox{ per } \left|x\right| < \frac{\pi}{2}$

$\mathrm{arcsinh} \left(x\right) = \sum^{\infin}_{n=0} \frac{(-1)^n (2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1}\quad\mbox{ per } \left| x \right| < 1$

$\mathrm{arctanh} \left(x\right) = \sum^{\infin}_{n=0} \frac{1}{2n+1} x^{2n+1}\quad\mbox{ per } \left| x \right| < 1$

Funzione W di Lambert:

$W_0(x) = \sum^{\infin}_{n=1} \frac{(-n)^{n-1}}{n!} x^n\quad\mbox{ per } \left| x \right| < \frac{1}{\mathrm{e}}$

I numeri B_k che compaiono negli sviluppi di tan(x) e tanh(x) sono i numeri di Bernoulli. Lo sviluppo binomiale si serve dei coefficienti binomiali. Gli E_k nello sviluppo della sec(x) sono i numeri di Eulero.

[modifica]

Calcoli delle serie di Taylor

Sono stati sviluppati molti metodi per il calcolo delle serie di Taylor per le molte funzioni analitiche utilizzate nella matematica e nelle sue applicazioni. Una strada consiste nell'utilizzare la serie di Taylor attraverso la sua definizione e generalizzare la forma dei coefficienti. Un'altra procede ad eseguire manipolazioni formali, come sostituzioni, moltiplicazioni o divisioni, addizioni o sottrazioni di serie di Taylor note per costruire la serie di Taylor di nuove funzioni, sfruttando le possibilità di manipolazione delle serie di potenze; in questo ambito può rivelarsi utile fare riferimento ai risultati riguardanti le serie ipergeometriche, le serie ipergeometriche basiche, i polinomi ortogonali e il calcolo umbrale. In taluni casi si riescono a derivare serie di Taylor applicando ripetutamente l'integrazione per parti.

Va anche osservato che per effettuare molte di queste elaborazioni possono essere molto utili gli odierni strumenti per il calcolo simbolico automatico (v. Sistemi di computer algebra).

Presentiamo ora due esempi di calcoli manuali. Cerchiamo di individuare la serie di Taylor centrata in 0 della funzione

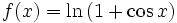$f(x)=\ln{(1+\cos{x})} \,$ .

Si parte dalla considerazione che

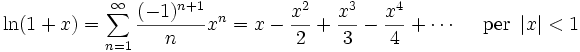
$\ln(1+x) = \sum^{\infin}_{n=1} \frac{(-1)^{n+1}}{n} x^n = x - {x^2\over 2}+{x^3 \over 3} - {x^4 \over 4} + \cdots \quad\mbox{ per } \left| x \right| < 1$

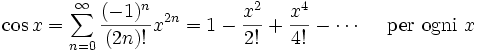$\cos x = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n)!} x^{2n} = 1 -{x^2\over 2!}+{x^4\over 4!}-\cdots \quad\mbox{ per ogni } x$ .

Ora si può semplicemente sostituire la seconda serie nella prima ottenendo

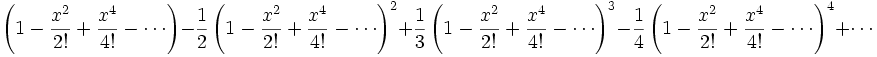$\left(1 -{x^2\over 2!}+{x^4\over 4!}-\cdots \right) - {1\over 2} \left(1 -{x^2\over 2!}+{x^4\over 4!}-\cdots \right)^2 + {1\over 3}\left(1 -{x^2\over 2!}+{x^4\over 4!}-\cdots\right)^3 - {1\over 4}\left(1 -{x^2\over 2!}+{x^4\over 4!}-\cdots\right)^4 + \cdots$ .

Sviluppando un adeguato numero di potenze mediante i coefficienti multinomiali si possono ottenere quanti si vogliono termini della serie di Taylor richiesta.

Come secondo esempio consideriamo la funzione

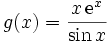$g(x)={x\,\mathrm{e}^x \over \sin{x}}$ .

Sappiamo che

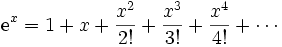
$\mathrm{e}^x = 1 + x + {x^2 \over 2!} + {x^3 \over 3!} + {x^4 \over 4!} + \cdots$

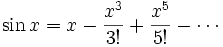$\sin{x} = x - {x^3 \over 3!} + {x^5 \over 5!} - \cdots$ .

Di conseguenza

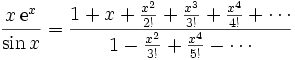${x\,\mathrm{e}^x \over \sin{x}} = { 1 + x + {x^2 \over 2!} + {x^3 \over 3!} + {x^4 \over 4!} + \cdots \over 1 - {x^2 \over 3!} + {x^4 \over 5!} - \cdots}$ .

Scriviamo la serie di potenze richiesta nella forma

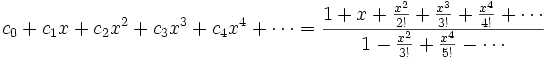$c_0 + c_1 x + c_2 x^2 + c_3 x^3 + c_4 x^4 + \cdots = {1 + x + {x^2 \over 2!} + {x^3 \over 3!} + {x^4 \over 4!} + \cdots \over 1 - {x^2 \over 3!} + {x^4 \over 5!} - \cdots}$ ;

Per questi coefficienti si trova

$1 + x + {x^2 \over 2!} + {x^3 \over 3!} + {x^4 \over 4!} + \cdots =$

$= \left(c_0 + c_1 x + c_2 x^2 + c_3 x^3 + c_4 x^4 + \cdots\right)\left(1 - {x^2 \over 3!} + {x^4 \over 5!} - \cdots\right)$

$=c_0 - {c_0 \over 3!}x^2 + {c_0\over 5!}x^4 + c_1x - {c_1 \over 3!}x^3 + {c_1\over 5!}x^5 + c_2 x^2 - {c_2 \over 3!} x^4 + {c_2 \over 5!} x^6 + c_3x^3-{c_3\over 3!}x^5 + c_4 x^4 + \cdots$

$=c_0 + c_1x + c_2 x^2 - {c_0 \over 3!}x^2 + c_3x^3- {c_1 \over 3!}x^3 + c_4 x^4 - {c_2 \over 3!} x^4 + {c_0 \over 5!} x^4 + \cdots$

In conclusione

$1 + x + {x^2 \over 2!} + {x^3 \over 3!} + {x^4 \over 4!} + \cdots =$

$=c_0 + c_1x + \left(c_2 - {c_0 \over 3!}\right)x^2 + \left(c_3-{c_1 \over 3!}\right)x^3 + \left(c_4-{c_2 \over 3!}+{c_0 \over 5!}\right)x^4 + \cdots$

e dal confronto dei coefficienti delle successive potenze si ottiene un sistema illimitatamente estendibile di equazioni lineari che evidentemente consente di individuare la serie della funzione proposta.

[modifica]