|
|
Trasformata di Fourier
(Suggerita da Alessandro Bernardini)
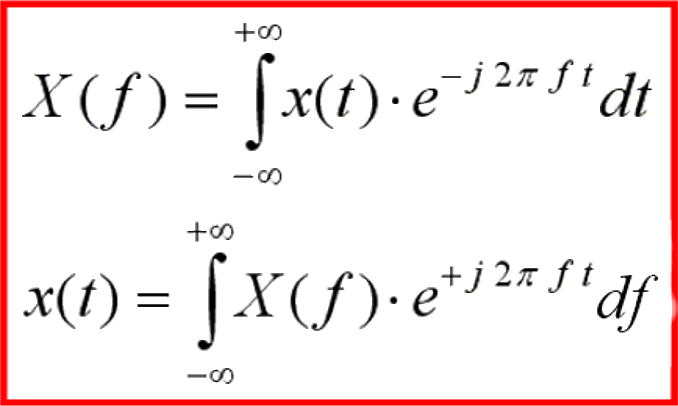
Già solo la scrittura di questa coppia di formule, con una perfetta simmetria fra la X(f) e la x(t), salvo nei segni più e meno che si scambiano, ne potrebbe giustificare l'inserimento in questa sezione dedicata appunto alle formule più belle. Ma oltre alla loro bellezza estetica, queste due formule sono di un'importanza assolutamente fondamentale in molti ambiti non solo della matematica, ma della scienza e della tecnica in generale.
Dal punto di vista formale, queste formule mostrano il passaggio dal dominio del tempo, x(t) appunto, al dominio della frequenza X(f), e viceversa. Se partiamo per esempio da un segnale sonoro, che è descritto istante per istante da una forma d'onda che abbia funzione x(t), grazie alla Trasformata di Fourier possiamo scomporre il segnale in tutte le sue armoniche ed ottenerne la cosiddetta "trasformata", ovvero una funzione X(f) che rappresenta lo stesso segnale di partenza descritto in un altro modo. Il bello è che (diciamo per quasi tutte le funzioni comunemente usate, perchè in realtà dal punto di vista matematico occorrerebbero molte considerazioni sulle funzioni x(t) ed X(f)) queste formule possono essere liberamente utilizzate per passare da un dominio all'altro a seconda del tipo di calcoli che si vogliono effettuare, ed il segnale, nell'una o nell'altra forma, resta sempre il medesimo!
Facciamo un esempio veramente banale per
intuire cosa significhi questa trasformazione. Quando noi parliamo o emettiamo
dei suoni, utilizziamo delle frequenze che variano fra i 20 ed i 20.000 Hz (e
gli animali arrivano a frequenze molto più alte!). Ebbene, grazie alla
Trasformata di Fourier potremmo per esempio pensare di registrare la nostra
voce, passare nel dominio della frequenza, quindi cancellare tutte le frequenze
al di sopra diciamo dei 3.000 Hz, quindi ritornare nel dominio del tempo.
Riascoltando la nostra voce modificata in questo modo la sentiremmo allora con
un tono molto più basso e cupo, e questo proprio in virtù dell'eliminazione
delle frequenze alte ottenuta grazie al passaggio in frequenza.
Ma i campi di applicazione della Trasformata di Fourier varcano i confini del
signal processing, infatti essa viene utilizzata per la progettazione di
circuiti elettronici, dispositivi di controllo, per la codifica di suoni,
immagini, ecc... ed inoltre le sue proprietà puramente matematiche vengono
sfruttate in un'infinità di teorie e dimostrazioni matematiche.
Anche se ci sarebbe da parlarne per pagine e pagine, esponiamo solamente un'altra formula di quasi pari importanza, che è quella della Serie di Fourier, che permette di scomporre un qualunque segnale periodico x(t) in una somma di infinite sinusoidi di ampiezza diversa:
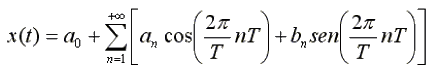
Alessandro Bernardini aggiunge:
L'uso delle trasformate di Fourier permette di pensare
un segnale qualsiasi come una somma o sovrapposizione di infinite sinusoidi con
la conseguenza che per determinare come un sistema reagisce ad un dato segnale è
sufficiente sapere come il sistema (supposto lineare) reagisce alla generica
sinusoide che compone il segnale e sommare tutti i risultati "parziali". Con
questo procedimento si perviene in modo molto più semplice alla risoluzione di
svariati problemi e si può anche agevolmente determinare come un sistema
(lineare) reagisce ad un segnale qualsiasi, una volta che siano fissate alcune
ipotesi sulle componenti di dato segnale. Ecco perchè, per esempio, siamo in
grado di sapere che una trasmittente radio è capace di trasmettere correttamente
ogni brano musicale e ogni voce umana e non soltanto alcune voci e non altre o
alcuni suoni e non altri (e, per inciso, ecco perchè possiamo anche sapere
quante "risorse" dobbiamo usare per trasmettere una voce "qualsiasi" in modo che
il tutto funzioni senza disturbi o interferenze, con un livello di qualità
adeguato e garantendo anche ad altri la possibilità di trasmettere "in
pace"...).