Diodati.org - Accessibilità e traduzioni dal W3C

Sponsor ufficiale di Diodati.org: Hosting a partire da 25 euro/anno | Domini a partire da 10,79 euro/anno | Server dedicati a partire da 120 euro/mese

Quest'algoritmo non distruttivo fu inventato nel 1952 dal matematico D.A. Huffman ed è un metodo di compressione particolarmente ingegnoso. Funziona in questo modo:

1. analizza il numero di ricorrenze di ciascun elemento costitutivo del file da comprimere: i singoli caratteri in un file di testo, i pixel in un file grafico.

2. Accomuna i due elementi meno frequenti trovati nel file in una categoria-somma che li rappresenta entrambi. Così ad esempio se A ricorre 8 volte e B 7 volte, viene creata la categoria-somma AB, dotata di 15 ricorrenze. Intanto i componenti A e B ricevono ciascuno un differente marcatore che li identifica come elementi entrati in un'associazione.

3. L'algoritmo identifica i due successivi elementi meno frequenti nel file e li riunisce in una nuova categoria-somma, usando lo stesso procedimento descritto al punto 2. Il gruppo AB può a sua volta entrare in nuove associazioni e costituire, ad esempio, la categoria CAB. Quando ciò accade, la A e la B ricevono un nuovo identificatore di associazione che finisce con l'allungare il codice che identificherà univocamente ciascuna delle due lettere nel file compresso che verrà generato.

4. Si crea per passaggi successivi un albero costituito da una serie di ramificazioni binarie, all'interno del quale appaiono con maggiore frequenza e in combinazioni successive gli elementi più rari all'interno del file, mentre appaiono più raramente gli elementi più frequenti. In base al meccanismo descritto, ciò fa sì che gli elementi rari all'interno del file non compresso siano associati ad un codice identificativo lungo, che si accresce di un elemento ad ogni nuova associazione. Gli elementi invece che si ripetono più spesso nel file originale sono anche i meno presenti nell'albero delle associazioni, sicché il loro codice identificativo sarà il più breve possibile.

5. Viene generato il file compresso, sostituendo a ciascun elemento del file originale il relativo codice prodotto al termine della catena di associazioni basata sulla frequenza di quell'elemento nel documento di partenza.

Il guadagno di spazio al termine della compressione è dovuto al fatto che gli elementi che si ripetono frequentemente sono identificati da un codice breve, che occupa meno spazio di quanto ne occuperebbe la loro codifica normale. Viceversa gli elementi rari nel file originale ricevono nel file compresso una codifica lunga, che può richiedere, per ciascuno di essi, uno spazio anche notevolmente maggiore di quello occupato nel file non compresso.

Dalla somma algebrica dello spazio guadagnato con la codifica breve degli elementi più frequenti e dello spazio perduto con la codifica lunga degli elementi più rari si ottiene il coefficiente di compressione prodotto dall'algoritmo Huffman. Da quanto detto si deduce che questo tipo di compressione è tanto più efficace quanto più ampie sono le differenze di frequenza degli elementi che costituiscono il file originale, mentre scarsi sono i risultati che si ottengono quando la distribuzione degli elementi è uniforme.

Un'ottima dimostrazione del funzionamento di questo algoritmo è visionabile su Internet all'indirizzo http://www.cs.sfu.ca/CC/365/li/squeeze/Huffman.html. Qui troverete un'applet java in grado di eseguire la generazione dell'albero delle associazioni, di produrre il codice compresso e di calcolare il coefficiente finale di compressione. Nelle due immagini sotto riportate, tratte dall'uso di questa applet, potete osservare l'albero generato dalla frequenza di ricorsività delle lettere costituenti un noto scioglilingua ed il risultato della compressione Huffman ottenuta.

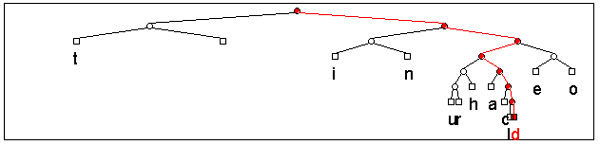
Fig. 2 – L'albero delle associazioni relativo al testo di uno scioglilingua. La struttura dell'albero mostra che le lettere d e  l sono le meno frequenti di tutte

Fig. 3 – La compressione ottenuta ha permesso un risparmio di spazio pari a quasi il 60%