Sesta puntata

Nella puntata precedente abbiamo visto che il problema di mettere in interazione elettroni/positroni coi fotoni si riduce a scrivere una certa "lagrangiana d'interazione", che consiste in un prodotto di quattro fattori:

1) una costante: la carica dell'elettrone 2) il potenziale (quadripotenziale) 3) il campo di Dirac 4) il suo coniugato.

In simboli: eAψψ-barrato.

Ora che abbiamo le "giuste" equazioni per i campi in interazione, occorre interpretarle e poi applicarle a problemi concreti.
Il problema è costituito dall'osservazione già fatta, che ora le equazioni non sono più lineari (questo deriva dal fatto che nella lagrangiana d'interazione figura il prodotto di tre campi, ma non posso spiegare di più).
Le equazioni non lineari sono sempre un problema, a meno che non sia possibile qualche approssimazione. L'approssimazione più ovvia si ha quando il termine d'interazione è piccolo, perché allora si può sperare che l'effetto dell'interazione sia modesto, e possa essere trattato come una "perturbazione" rispetto al caso in cui l'interazione non c'è.
Attenzione alla parola magica: "perturbazione"! Vedremo che nel seguito tutto ruoterà attorno a quest'idea, croce e delizia del fisico teorico...

Se l'interazione sia grande o piccola, dipende dal valore di un parametro, che figura nella suddetta: la carica e.
Ora e non è un numero puro (è la carica dell'elettrone) e non ha perciò senso chiedersi se sia grande o piccolo; ma è facile ricavarne un numero puro, anzi l'abbiamo già visto: la costante di struttura fina  2πe²/hc. Questa è piccola, e ci dà buone speranze.

Ora debbo fare qualche affermazione che non mi è possibile giustificare decentemente, circa l'interpretazione della nostra interazione.
Compare il potenziale (che fa le veci del campo e.m.): ciò significa che il processo più semplice possibile prodotto da quell'interazione comporterà la creazione o la distruzione di un fotone.
Compare il campo ψ accompagnato da ψ -bar: allora per quanto riguarda elettroni/positroni il processo più semplice possibile non è la nascita o la morte di un singolo elettrone/positrone, ma saranno sempre coinvolte due particelle, nei modi seguenti:

-  un elettrone scompare in  qualche punto dello sp.-tempo,  e ne nasce un altro  nello stesso punto -  un positrone scompare " " " -  nascono insieme un elettrone e un positrone. -  scompaiono insieme un elettrone e un positrone.

Notate che in tutti i casi la carica si conserva, come è d'obbligo.

I primi due processi possono essere descritti in modo equivalente dicendo che un elettrone/positrone modifica il suo stato di moto (impulso ed energia). Ma come è possibile questo?
Risposta: perché allo stesso tempo (e nello stesso punto) è apparso o scomparso un fotone, che si porta via (o fornisce) impulso ed energia nella misura necessaria per la conservazione. Analogo discorso negli altri due casi.

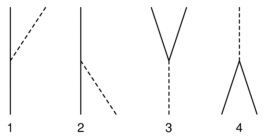
Mettiamo tutto insieme, e ritroviamo proprio i processi elementari che avevamo indicato nella quarta puntata, e che ora riscrivo:

1)  un elettrone (o un positrone) può emettere un fotone 2)  " " " assorbire " 3)  un fotone può dar luogo a una coppia elettrone-positrone 4)  una coppia si può annichilare in un fotone.

Perfetto: fila tutto a meraviglia, e non c'è che mettere la teoria al lavoro...
Notate che tutto questo, e anche parte di ciò che segue, è stato fatto prima del 1930: giusto per inquadrare la storia nel suo tempo.

Siamo ora in possesso della teoria dell'interazione tra fotoni ed elettroni, che non è altro che l'elettrodinamica quantistica oggetto di tutto il nostro discorso. Eppure il discorso non è ancora finito: come mai? La ragione è che la teoria così costruita è ancora incompleta, per un motivo che vedremo in seguito: per ricordare ciò, la indicherò con QED1 (da leggersi "QED in prima approssimazione").

Nel decennio 1930-40 la teoria QED1 fu messa alla prova, calcolando con essa tutto il calcolabile, e trovando sempre completo accordo sia con i dati sperimentali, dove disponibili, sia con la teoria semiclassica, dove questa era applicabile. (Ricordiamo: nella teoria semiclassica i fotoni non esistono: il campo e.m. è quello di Maxwell.)

Solo per dare qualche esempio:

1. Fu studiata l'emissione e l'assorbimento di fotoni da parte di atomi, ritrovando sia le formule della teoria semiclassica, sia l'emissione spontanea (che come ricorderete la teoria semiclassica non poteva spiegare). C'è anche da dire che QED1 fornisce una visione integrata dei due processi di emissione spontanea e indotta (ovvero stimolata), fornendo inoltre tra le loro probabilità esattamente il rapporto che Einstein aveva previsto dal 1917 (notate: quando non esisteva neppure la meccanica quantistica!)
È appena il caso di ricordare che l'emissione stimolata sta alla base del funzionamento dei laser, che sarebbero stati inventati solo 30 anni dopo...

2. Furono calcolate e verificate le modalità dell'"effetto Compton", nel quale un fotone urta un elettrone fermo (o quasi) e viene riemesso con energia minore, la residua energia essendo acquisita dall'elettrone. L'effetto Compton era noto dal 1925, ma non poteva essere spiegato dalla teoria semiclassica.

È il caso di soffermarsi sull'effetto Compton, perché si presta bene a mostrare alcune caratteristiche di QED1.
Nello stato iniziale abbiamo un elettrone e un fotone; in quello finale lo stesso, anche se tanto l'elettrone quanto il fotone avranno energie diversa da prima, e si muoveranno in direzioni differenti.
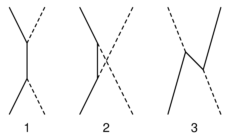
Ma come si arriva dallo stato iniziale a quello finale? Ci si deve arrivare attraverso uno o più dei 4 processi elementari visti sopra, e si vede facilmente che i processi coinvolti debbono essere due, dato che in ciascun processo elementare un solo fotone appare o scompare. Dovremo qui far scomparire il fotone iniziale, e far apparire quello finale: ma non è determinato l'ordine temporale in cui i due eventi avvengono. Può darsi che prima venga assobito il fotone iniziale, e poi venga emesso quello finale (fig. 1) ma può benissimo accadere che prima venga emesso il fotone finale (e così abbiamo per un certo tempo due fotoni) e poi scompaia quello iniziale (fig. 2).

Inoltre la scomparsa del fotone iniziale può avvenire in due modi: a) l'elettrone assorbe il fotone (figure 1 e 2) b) il fotone crea una coppia (fig. 3). Le figure che ho disegnato qui accanto sono i famosi diagrammi di Feynman, che opportunamente arricchiti d'informazioni su impulsi ed energie delle varie particelle, sono la base di tutti i calcoli di QED (e oltre).

Uno degli aspetti affascinanti di QED è che questa molteplicità di possibilità non va considerata espressamente: vengono tutte inglobate in un unico calcolo, che le mette in conto automaticamente (questo non è proprio preciso, ma sarebbe troppo lungo - anche se non complicato - spiegare come stanno davvero le cose).
Il risultato finale è una formula, nota come "formula di Klein-Nishina", che ci dice qual è la probabilità che il fotone esca in un certa direzione e con una certa energia.

3. Continuando con i calcoli e verifiche: ricordate che una carica accelerata irraggia? Ebbene, QED1 è in grado di calcolare anche questo fenomeno (che è tradizionalmente noto col termine tedesco Bremsstrahlung): si riesce a prevedere la probabilità che vengano emessi uno o più fotoni, di quali energie, in quali direzioni...

Potrei continuare, ma non è il caso: il nocciolo del discorso è che sembra che tutto fili a perfezione. E invece non è così, ma tanto per cambiare ne riparleremo nella prossima puntata.

(Fine della sesta puntata)