Breve storia dell'elettrodinamica quantistica
Elio Fabri
Ultima revisione: 2-5-98
Settima puntata
 Dicevo nella puntata precedente che sembra che
tutto fili a perfezione, ma non è così. Debbo ora spiegare che
cosa intendevo dire.
Dicevo nella puntata precedente che sembra che
tutto fili a perfezione, ma non è così. Debbo ora spiegare che
cosa intendevo dire.
 A questo scopo dobbiamo fare un passo
indietro, tornando all'inizio della sesta puntata, dove ho detto che le
equazioni giuste di QED sono troppo complicate per darne una soluzione esatta,
ma per fortuna si può procedere trattando l'interazione tra elettroni e
fotoni come una perturbazione, grazie alla piccolezza della costante di
struttura fina.
A questo scopo dobbiamo fare un passo
indietro, tornando all'inizio della sesta puntata, dove ho detto che le
equazioni giuste di QED sono troppo complicate per darne una soluzione esatta,
ma per fortuna si può procedere trattando l'interazione tra elettroni e
fotoni come una perturbazione, grazie alla piccolezza della costante di
struttura fina.
 Ma non ho mai detto in che consista esattamente
l'approssimazione, anche se le ho dato un nome: QED1. È ora il momento
di colmare la lacuna.
Ma non ho mai detto in che consista esattamente
l'approssimazione, anche se le ho dato un nome: QED1. È ora il momento
di colmare la lacuna.
 L'approssimazione consiste in questo: che per
qualunque processo fisico che c'interessa studiamo solo il modo più
semplice di realizzarlo (il diagramma di Feynman col minor numero di vertici).
Spieghiamoci con un esempio: ancora l'effetto Compton.
L'approssimazione consiste in questo: che per
qualunque processo fisico che c'interessa studiamo solo il modo più
semplice di realizzarlo (il diagramma di Feynman col minor numero di vertici).
Spieghiamoci con un esempio: ancora l'effetto Compton.
 Abbiamo visto che possiamo supporre (ci sono
altre possibilità) che l'elettrone assorba il fotone, restando solo
soletto in uno stato virtuale, e poi lo riemetta. Nel diagramma ci sono due
vertici, e nel gergo dei fisici teorici questo si esprime dicendo che stiamo
studiando un processo di secondo ordine.
Abbiamo visto che possiamo supporre (ci sono
altre possibilità) che l'elettrone assorba il fotone, restando solo
soletto in uno stato virtuale, e poi lo riemetta. Nel diagramma ci sono due
vertici, e nel gergo dei fisici teorici questo si esprime dicendo che stiamo
studiando un processo di secondo ordine. Per inciso, la probabilità di un processo di secondo ordine è
proporzionale al quadrato della costante di struttura fina (per uno di terzo
ordine sarebbe proporzionale al suo cubo, ecc.).
Per inciso, la probabilità di un processo di secondo ordine è
proporzionale al quadrato della costante di struttura fina (per uno di terzo
ordine sarebbe proporzionale al suo cubo, ecc.).
 Ma possiamo considerare situazioni più
complicate:
Ma possiamo considerare situazioni più
complicate:
| a) |
L'elettrone virtuale può emettere un fotone e
riassorbirlo poco dopo, prima di emettere il fotone finale
(fig. 1). Questo è un fotone virtuale, per la stessa
ragione per cui era virtuale l'elettrone: perché nella
sua emissione/assorbimento non si può conservare insieme
energia e impulso, e allo stesso tempo rispettare la massa
(nulla) del fotone. |
| b) |
La stessa cosa può accadere prima che venga assorbito il fotone
iniziale (fig. 2) oppure dopo che è stato emesso quello
finale. che venga assorbito il fotone
iniziale (fig. 2) oppure dopo che è stato emesso quello
finale. |
| 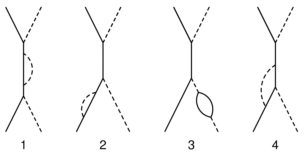 |
| c) |
Il fotone iniziale (o quello finale) possono dar luogo a una
coppia elettrone-positrone (fig. 3), che poco dopo si annichila
di nuovo in un fotone. |
| d) |
L'elettrone iniziale può emettere un fotone virtuale, poi
assorbire quello reale incidente, poi riassorbire quello
virtuale (fig. 4). |
| e) |
Ci sono varie altre possibilità. |
|
 Bene, direte voi, si tratta solo di armarsi
di pazienza. Notate che tutti gli esempi che ho fatto hanno solo 4 vertici:
sono processi di quarto
Bene, direte voi, si tratta solo di armarsi
di pazienza. Notate che tutti gli esempi che ho fatto hanno solo 4 vertici:
sono processi di quarto ordine, e sono
già parecchi; ma poi si potrebbero considerare quelli di sesto ordine,
ecc., che diventano sempre più numerosi.
ordine, e sono
già parecchi; ma poi si potrebbero considerare quelli di sesto ordine,
ecc., che diventano sempre più numerosi.
 Però le corrispondenti
probabilità contengono la costante di struttura fina con potenze sempre
maggiori; e dato che è piccola, queste potenze sono sempre più
piccole. Quindi si può sperare che i processi di ordine superiore siano
via via meno importanti, per cui se ci si accontenta di una determinata
approssimazione ci si potrà arrestare a un certo ordine. Il calcolo
sarà molto noioso, ma consisterà di un numero finito (anche se
grande) di operazioni. E i calcolatori che sono stati inventati a fare?
Però le corrispondenti
probabilità contengono la costante di struttura fina con potenze sempre
maggiori; e dato che è piccola, queste potenze sono sempre più
piccole. Quindi si può sperare che i processi di ordine superiore siano
via via meno importanti, per cui se ci si accontenta di una determinata
approssimazione ci si potrà arrestare a un certo ordine. Il calcolo
sarà molto noioso, ma consisterà di un numero finito (anche se
grande) di operazioni. E i calcolatori che sono stati inventati a fare?
 Ahinoi, le cose non sono così semplici
(si fa per dire).
Ahinoi, le cose non sono così semplici
(si fa per dire).
 Consideriamo il primo degli esempi che ho
dato. Abbiamo un solo fotone virtuale: quale sarà il suo impulso e la
sua energia?
Consideriamo il primo degli esempi che ho
dato. Abbiamo un solo fotone virtuale: quale sarà il suo impulso e la
sua energia?
 Notate che impulso ed energia delle particelle
reali,
Notate che impulso ed energia delle particelle
reali, iniziali e finali, non sono
incognite: sono i dati del problema. Anche l'elettrone virtuale nel processo
di secondo ordine ha impulso ed energia determinati dalla conservazione (ed
è virtuale perché con quell'impulso e quell'energia ha una massa
"sbagliata").
iniziali e finali, non sono
incognite: sono i dati del problema. Anche l'elettrone virtuale nel processo
di secondo ordine ha impulso ed energia determinati dalla conservazione (ed
è virtuale perché con quell'impulso e quell'energia ha una massa
"sbagliata").
 Ma se ci sono due o più particelle
virtuali, le leggi di conservazione non bastano a determinarne impulso ed
energia, che possono quindi essere scelti a piacere. Come possiamo fare i
calcoli se ci restano delle incognite indeterminate?
Ma se ci sono due o più particelle
virtuali, le leggi di conservazione non bastano a determinarne impulso ed
energia, che possono quindi essere scelti a piacere. Come possiamo fare i
calcoli se ci restano delle incognite indeterminate?
 La regola che vale non solo in QED, ma in
tutta la m.q., è questa: quando in uno stato virtuale c'è una
grandezza indeterminata, il calcolo va fatto sommando
La regola che vale non solo in QED, ma in
tutta la m.q., è questa: quando in uno stato virtuale c'è una
grandezza indeterminata, il calcolo va fatto sommando su tutte le possibilità.
su tutte le possibilità.
 Poiché nel nostro caso le
possibilità sono un continuo di valori, la somma sarà in effetti
un integrale, ma questo importa poco. Quello che invece importa molto è
che cosa succede appena si tenta di calcolare l'integrale: si trova un
risultato infinito
Poiché nel nostro caso le
possibilità sono un continuo di valori, la somma sarà in effetti
un integrale, ma questo importa poco. Quello che invece importa molto è
che cosa succede appena si tenta di calcolare l'integrale: si trova un
risultato infinito ! E lo stesso succede
per tutti
! E lo stesso succede
per tutti i processi virtuali, quelli che ho descritto, e gli
altri che si possono immaginare.
i processi virtuali, quelli che ho descritto, e gli
altri che si possono immaginare.
 Ora sì che siamo nei guai: nel
tentativo di migliorare l'approssimazione QED1, siamo finiti a non saper
calcolare un bel niente: infinito dappertutto!
Ora sì che siamo nei guai: nel
tentativo di migliorare l'approssimazione QED1, siamo finiti a non saper
calcolare un bel niente: infinito dappertutto!
 Col suo stile inimitabilmente antiaccademico,
Feynman ha descritto la situazione dicendo: "la teoria ha sbattuto la
faccia per terra".
Col suo stile inimitabilmente antiaccademico,
Feynman ha descritto la situazione dicendo: "la teoria ha sbattuto la
faccia per terra".
 Così stavano le cose alla fine degli
anni '30; ma niente paura, la storia ha il giusto lieto fine. Alla prossima
puntata.
Così stavano le cose alla fine degli
anni '30; ma niente paura, la storia ha il giusto lieto fine. Alla prossima
puntata.
(Fine della settima puntata)
 A questo scopo dobbiamo fare un passo
indietro, tornando all'inizio della sesta puntata, dove ho detto che le
equazioni giuste di QED sono troppo complicate per darne una soluzione esatta,
ma per fortuna si può procedere trattando l'interazione tra elettroni e
fotoni come una perturbazione, grazie alla piccolezza della costante di
struttura fina.
A questo scopo dobbiamo fare un passo
indietro, tornando all'inizio della sesta puntata, dove ho detto che le
equazioni giuste di QED sono troppo complicate per darne una soluzione esatta,
ma per fortuna si può procedere trattando l'interazione tra elettroni e
fotoni come una perturbazione, grazie alla piccolezza della costante di
struttura fina. Ma non ho mai detto in che consista esattamente
l'approssimazione, anche se le ho dato un nome: QED1. È ora il momento
di colmare la lacuna.
Ma non ho mai detto in che consista esattamente
l'approssimazione, anche se le ho dato un nome: QED1. È ora il momento
di colmare la lacuna. L'approssimazione consiste in questo: che per
qualunque processo fisico che c'interessa studiamo solo il modo più
semplice di realizzarlo (il diagramma di Feynman col minor numero di vertici).
Spieghiamoci con un esempio: ancora l'effetto Compton.
L'approssimazione consiste in questo: che per
qualunque processo fisico che c'interessa studiamo solo il modo più
semplice di realizzarlo (il diagramma di Feynman col minor numero di vertici).
Spieghiamoci con un esempio: ancora l'effetto Compton.
