4. Il terzo principio
 Questo intervento del terzo principio
è caratteristico di tutti i casi in cui si fanno "trasmettere" forze da
un corpo a un altro, come con i fili, ecc. (Nel nostro caso è
però essenziale anche il primo principio: se C non fosse fermo, niente
garantirebbe il risultato cercato F'=P).
Questo intervento del terzo principio
è caratteristico di tutti i casi in cui si fanno "trasmettere" forze da
un corpo a un altro, come con i fili, ecc. (Nel nostro caso è
però essenziale anche il primo principio: se C non fosse fermo, niente
garantirebbe il risultato cercato F'=P).
 È molto comune trovare un ragionamento
simile al precedente, usato alla rovescia, e in modo errato,
È molto comune trovare un ragionamento
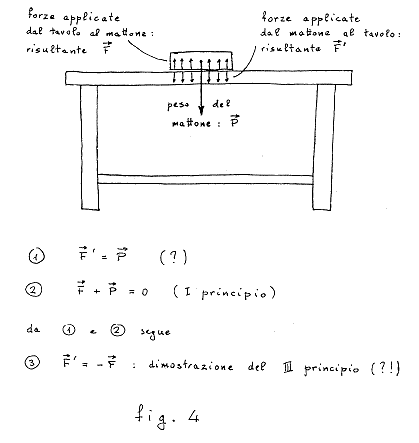
simile al precedente, usato alla rovescia, e in modo errato, come una prova del terzo principio. Si ragiona
così (fig. 4): "Se un mattone è appoggiato su di un tavolo,
esso applica al tavolo una forza uguale al suo peso (!). Ma il mattone
è fermo, e questo dimostra che il tavolo reagisce con una forza uguale
e contraria, c.d.d." (?!).
come una prova del terzo principio. Si ragiona
così (fig. 4): "Se un mattone è appoggiato su di un tavolo,
esso applica al tavolo una forza uguale al suo peso (!). Ma il mattone
è fermo, e questo dimostra che il tavolo reagisce con una forza uguale
e contraria, c.d.d." (?!).
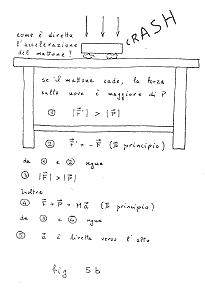
 Per mostrare l'errore, poggiamo il mattone
su quattro uova, che lo reggeranno benissimo (fig. 5a). Poi solleviamo il
mattone di qualche centimetro, e lasciamolo cadere (fig. 5b): la frittata che
ne risulta dimostra che solo quando il mattone è in quiete posso dire
che esso agisce sulle uova con una forza uguale al suo peso. Dunque la prima
affermazione è falsa, e non può servire come premessa al
ragionamento che segue. Non per questo il terzo principio cessa di essere
valido: anzi può essere usato per provare che durante la rottura delle
uova il mattone un'accelerazione diretta verso l'alto (il che a prima vista
non è affatto ovvio).
Per mostrare l'errore, poggiamo il mattone
su quattro uova, che lo reggeranno benissimo (fig. 5a). Poi solleviamo il
mattone di qualche centimetro, e lasciamolo cadere (fig. 5b): la frittata che
ne risulta dimostra che solo quando il mattone è in quiete posso dire
che esso agisce sulle uova con una forza uguale al suo peso. Dunque la prima
affermazione è falsa, e non può servire come premessa al
ragionamento che segue. Non per questo il terzo principio cessa di essere
valido: anzi può essere usato per provare che durante la rottura delle
uova il mattone un'accelerazione diretta verso l'alto (il che a prima vista
non è affatto ovvio).
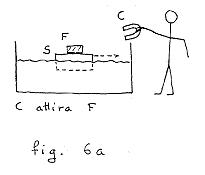
 Non è forse inutile illustrare
un'altra tipica pseudo-dimostrazione del terzo principio, dove l'errore
è analogo, ma più riposto. Si poggia un pezzo di ferro su un
sughero che galleggia nell'acqua di una bacinella, e si avvicina una calamita
(fig. 6a): il sughero, col ferro sopra, si muove, dimostrando che la calamita
attira il ferro.
Non è forse inutile illustrare
un'altra tipica pseudo-dimostrazione del terzo principio, dove l'errore
è analogo, ma più riposto. Si poggia un pezzo di ferro su un
sughero che galleggia nell'acqua di una bacinella, e si avvicina una calamita
(fig. 6a): il sughero, col ferro sopra, si muove, dimostrando che la calamita
attira il ferro.
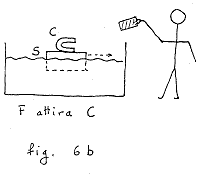
 Si mette ora la calamita sul sughero, e si
tiene il ferro in mano (fig. 6b): questa volta è la calamita (col
sughero) a muoversi, e dunque il ferro attira la calamita.
Si mette ora la calamita sul sughero, e si
tiene il ferro in mano (fig. 6b): questa volta è la calamita (col
sughero) a muoversi, e dunque il ferro attira la calamita.
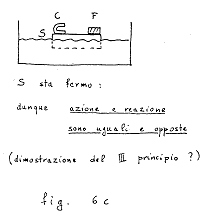
 A questo punto, per confrontare le due
attrazioni, si posano ferro e calamita sul sughero, si vede che tutto resta
fermo (fig. 6c): applicando il primo principio si conclude che le due forze
in questione si fanno equilibrio (?!).
A questo punto, per confrontare le due
attrazioni, si posano ferro e calamita sul sughero, si vede che tutto resta
fermo (fig. 6c): applicando il primo principio si conclude che le due forze
in questione si fanno equilibrio (?!).
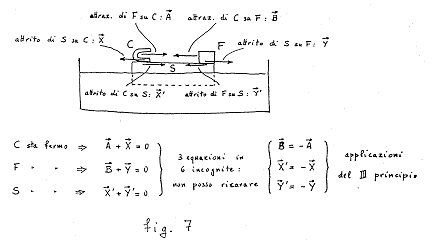
 Il ragionamento esatto è mostrato in
fig. 7: si vede che occorre tener conto di altre 4 forze, e perciò si
hanno in tutto 6 forze incognite. Le condizioni di equilibrio danno 3
equazioni, applicandole rispettivamente al ferro, alla calamita e al sughero:
ma le 3 equazioni così ottenute non permettono di dedurre la
conclusione voluta (e naturalmente nemmeno le altre due relazioni che si
ottengono dal terzo principio nel nostro caso).
Il ragionamento esatto è mostrato in
fig. 7: si vede che occorre tener conto di altre 4 forze, e perciò si
hanno in tutto 6 forze incognite. Le condizioni di equilibrio danno 3
equazioni, applicandole rispettivamente al ferro, alla calamita e al sughero:
ma le 3 equazioni così ottenute non permettono di dedurre la
conclusione voluta (e naturalmente nemmeno le altre due relazioni che si
ottengono dal terzo principio nel nostro caso).
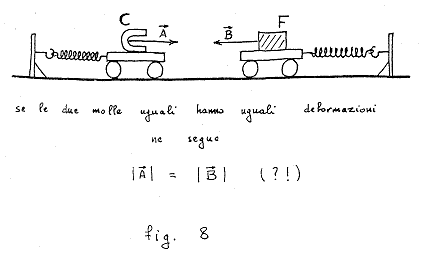
 Sempre sullo stesso problema, un'altra
versione che sembra quasi inattaccabile è mostrata in fig. 8: questa
volta uso due dinamometri uguali per misurare le forze, e se le deformazioni
sono uguali non c'è dubbio che ho dimostrato il terzo principio
(?!).
Sempre sullo stesso problema, un'altra
versione che sembra quasi inattaccabile è mostrata in fig. 8: questa
volta uso due dinamometri uguali per misurare le forze, e se le deformazioni
sono uguali non c'è dubbio che ho dimostrato il terzo principio
(?!).
 Ormai posso lasciare al lettore divertimento
di scoprire l'errore, e tornare invece al tema principale.
Ormai posso lasciare al lettore divertimento
di scoprire l'errore, e tornare invece al tema principale.

 Questo intervento del terzo principio
è caratteristico di tutti i casi in cui si fanno "trasmettere" forze da
un corpo a un altro, come con i fili, ecc. (Nel nostro caso è
però essenziale anche il primo principio: se C non fosse fermo, niente
garantirebbe il risultato cercato F'=P).
Questo intervento del terzo principio
è caratteristico di tutti i casi in cui si fanno "trasmettere" forze da
un corpo a un altro, come con i fili, ecc. (Nel nostro caso è
però essenziale anche il primo principio: se C non fosse fermo, niente
garantirebbe il risultato cercato F'=P). È molto comune trovare un ragionamento
simile al precedente, usato alla rovescia, e in modo errato,
È molto comune trovare un ragionamento
simile al precedente, usato alla rovescia, e in modo errato, come una prova del terzo principio. Si ragiona
così (fig. 4): "Se un mattone è appoggiato su di un tavolo,
esso applica al tavolo una forza uguale al suo peso (!). Ma il mattone
è fermo, e questo dimostra che il tavolo reagisce con una forza uguale
e contraria, c.d.d." (?!).
come una prova del terzo principio. Si ragiona
così (fig. 4): "Se un mattone è appoggiato su di un tavolo,
esso applica al tavolo una forza uguale al suo peso (!). Ma il mattone
è fermo, e questo dimostra che il tavolo reagisce con una forza uguale
e contraria, c.d.d." (?!).

 Per mostrare l'errore, poggiamo il mattone
su quattro uova, che lo reggeranno benissimo (fig. 5a). Poi solleviamo il
mattone di qualche centimetro, e lasciamolo cadere (fig. 5b): la frittata che
ne risulta dimostra che solo quando il mattone è in quiete posso dire
che esso agisce sulle uova con una forza uguale al suo peso. Dunque la prima
affermazione è falsa, e non può servire come premessa al
ragionamento che segue. Non per questo il terzo principio cessa di essere
valido: anzi può essere usato per provare che durante la rottura delle
uova il mattone un'accelerazione diretta verso l'alto (il che a prima vista
non è affatto ovvio).
Per mostrare l'errore, poggiamo il mattone
su quattro uova, che lo reggeranno benissimo (fig. 5a). Poi solleviamo il
mattone di qualche centimetro, e lasciamolo cadere (fig. 5b): la frittata che
ne risulta dimostra che solo quando il mattone è in quiete posso dire
che esso agisce sulle uova con una forza uguale al suo peso. Dunque la prima
affermazione è falsa, e non può servire come premessa al
ragionamento che segue. Non per questo il terzo principio cessa di essere
valido: anzi può essere usato per provare che durante la rottura delle
uova il mattone un'accelerazione diretta verso l'alto (il che a prima vista
non è affatto ovvio).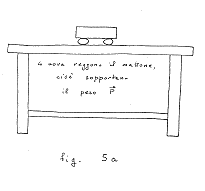
 Non è forse inutile illustrare
un'altra tipica pseudo-dimostrazione del terzo principio, dove l'errore
è analogo, ma più riposto. Si poggia un pezzo di ferro su un
sughero che galleggia nell'acqua di una bacinella, e si avvicina una calamita
(fig. 6a): il sughero, col ferro sopra, si muove, dimostrando che la calamita
attira il ferro.
Non è forse inutile illustrare
un'altra tipica pseudo-dimostrazione del terzo principio, dove l'errore
è analogo, ma più riposto. Si poggia un pezzo di ferro su un
sughero che galleggia nell'acqua di una bacinella, e si avvicina una calamita
(fig. 6a): il sughero, col ferro sopra, si muove, dimostrando che la calamita
attira il ferro.
 Si mette ora la calamita sul sughero, e si
tiene il ferro in mano (fig. 6b): questa volta è la calamita (col
sughero) a muoversi, e dunque il ferro attira la calamita.
Si mette ora la calamita sul sughero, e si
tiene il ferro in mano (fig. 6b): questa volta è la calamita (col
sughero) a muoversi, e dunque il ferro attira la calamita.
 A questo punto, per confrontare le due
attrazioni, si posano ferro e calamita sul sughero, si vede che tutto resta
fermo (fig. 6c): applicando il primo principio si conclude che le due forze
in questione si fanno equilibrio (?!).
A questo punto, per confrontare le due
attrazioni, si posano ferro e calamita sul sughero, si vede che tutto resta
fermo (fig. 6c): applicando il primo principio si conclude che le due forze
in questione si fanno equilibrio (?!).
 Il ragionamento esatto è mostrato in
fig. 7: si vede che occorre tener conto di altre 4 forze, e perciò si
hanno in tutto 6 forze incognite. Le condizioni di equilibrio danno 3
equazioni, applicandole rispettivamente al ferro, alla calamita e al sughero:
ma le 3 equazioni così ottenute non permettono di dedurre la
conclusione voluta (e naturalmente nemmeno le altre due relazioni che si
ottengono dal terzo principio nel nostro caso).
Il ragionamento esatto è mostrato in
fig. 7: si vede che occorre tener conto di altre 4 forze, e perciò si
hanno in tutto 6 forze incognite. Le condizioni di equilibrio danno 3
equazioni, applicandole rispettivamente al ferro, alla calamita e al sughero:
ma le 3 equazioni così ottenute non permettono di dedurre la
conclusione voluta (e naturalmente nemmeno le altre due relazioni che si
ottengono dal terzo principio nel nostro caso).
 Sempre sullo stesso problema, un'altra
versione che sembra quasi inattaccabile è mostrata in fig. 8: questa
volta uso due dinamometri uguali per misurare le forze, e se le deformazioni
sono uguali non c'è dubbio che ho dimostrato il terzo principio
(?!).
Sempre sullo stesso problema, un'altra
versione che sembra quasi inattaccabile è mostrata in fig. 8: questa
volta uso due dinamometri uguali per misurare le forze, e se le deformazioni
sono uguali non c'è dubbio che ho dimostrato il terzo principio
(?!).
 Ormai posso lasciare al lettore divertimento
di scoprire l'errore, e tornare invece al tema principale.
Ormai posso lasciare al lettore divertimento
di scoprire l'errore, e tornare invece al tema principale.