Breve storia dell'elettrodinamica quantistica
Elio Fabri
Ultima revisione: 2-5-98
Quarta puntata
 Ma come mai i positroni non erano stati visti
prima? Che proprietà hanno?
Ma come mai i positroni non erano stati visti
prima? Che proprietà hanno?
 La risposta alla seconda domanda è molto
semplice: sono in tutto e per tutto uguali agli elettroni, salvo per il segno
della carica. In particolare, hanno la stessa massa, spin, momento
magnetico.
La risposta alla seconda domanda è molto
semplice: sono in tutto e per tutto uguali agli elettroni, salvo per il segno
della carica. In particolare, hanno la stessa massa, spin, momento
magnetico.
 Non erano stati visti, prima di tutto
perché in natura sono molto rari (almeno nel nostro mondo...). La
ragione è che ci sono troppi elettroni: un positrone che attraversi
della materia, anche un gas molto rarefatto, prima o poi passa vicino a un
elettrone, e si produce un fenomeno caratteristico: le due particelle
scompaiono e si producono due o più fotoni ("annichilazione"
di una coppia elettrone-positrone).
Non erano stati visti, prima di tutto
perché in natura sono molto rari (almeno nel nostro mondo...). La
ragione è che ci sono troppi elettroni: un positrone che attraversi
della materia, anche un gas molto rarefatto, prima o poi passa vicino a un
elettrone, e si produce un fenomeno caratteristico: le due particelle
scompaiono e si producono due o più fotoni ("annichilazione"
di una coppia elettrone-positrone).
 È usata spesso, in questo caso,
l'espressione "conversione di massa in energia": espressione che a
me piace poco e preferisco non usare, perché trovo che aiuti molto a
confondere le idee. Ma questa è una divagazione che non posso
permettermi...
È usata spesso, in questo caso,
l'espressione "conversione di massa in energia": espressione che a
me piace poco e preferisco non usare, perché trovo che aiuti molto a
confondere le idee. Ma questa è una divagazione che non posso
permettermi...
 Non bisogna però equivocare: il
positrone non è una particella instabile, come i mesoni o il neutrone,
che lasciati a sé si disintegrano spontaneamente in altre particelle.
Un positrone in uno spazio vuoto è perfettamente stabile, tanto
è vero che oggi si producono senza problemi fasci di positroni: il solo
requisito è che possano muoversi in un ambiente dove non incontrino
elettroni.
Non bisogna però equivocare: il
positrone non è una particella instabile, come i mesoni o il neutrone,
che lasciati a sé si disintegrano spontaneamente in altre particelle.
Un positrone in uno spazio vuoto è perfettamente stabile, tanto
è vero che oggi si producono senza problemi fasci di positroni: il solo
requisito è che possano muoversi in un ambiente dove non incontrino
elettroni.
 Come si possono trovare allora dei positroni,
per es. nei raggi cosmici?
Come si possono trovare allora dei positroni,
per es. nei raggi cosmici?
 Il meccanismo più comune per produrli
è la "creazione di coppie": il processo inverso
dell'annichilazione. Da un fotone di energia sufficientemente alta (almeno 1
MeV) può "nascere" una coppia elettrone-positrone, che appena
nati se ne vanno ciascuno per i fatti suoi.
Il meccanismo più comune per produrli
è la "creazione di coppie": il processo inverso
dell'annichilazione. Da un fotone di energia sufficientemente alta (almeno 1
MeV) può "nascere" una coppia elettrone-positrone, che appena
nati se ne vanno ciascuno per i fatti suoi.
 (Dovrei essere preciso, e spiegare che un fotone
solo soletto non può produrre una coppia, ma ha bisogno di un altro
fotone o di un campo elettrostatico, ad es. quello di un nucleo; ma la
precisazione non è essenziale per ciò che segue.)
(Dovrei essere preciso, e spiegare che un fotone
solo soletto non può produrre una coppia, ma ha bisogno di un altro
fotone o di un campo elettrostatico, ad es. quello di un nucleo; ma la
precisazione non è essenziale per ciò che segue.)
 È importante riassumere ora l'insieme
dei processi elementari che coinvolgono elettroni, positroni e fotoni:
È importante riassumere ora l'insieme
dei processi elementari che coinvolgono elettroni, positroni e fotoni:
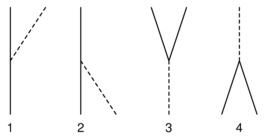
| 1)
| un elettrone
| (o un positrone)
| può
| emettere
| un fotone
|
| 2)
| "
| "
| "
| assorbire
| "
|
| 3)
| un fotone può dar luogo a una coppia
elettrone-positrone
|
| 4)
| una coppia si può annichilare in un fotone.
|
| 
|
|
 Obiezione, Vostro Onore: Ella ha
appena detto che l'annichilazione dà luogo a due o
più fotoni, non uno solo! Obiezione, Vostro Onore: Ella ha
appena detto che l'annichilazione dà luogo a due o
più fotoni, non uno solo!
 Obiezione accolta e respinta allo
stesso tempo. Obiezione accolta e respinta allo
stesso tempo.
 È vero: il processo
osservabile è quello, con due o più fotoni finali.
Ma può essere visto come composizione di due processi
più elementari: È vero: il processo
osservabile è quello, con due o più fotoni finali.
Ma può essere visto come composizione di due processi
più elementari:
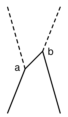
|
| a)
| un elettrone (positrone) emette un fotone
|
| b)
| dopo di ciò si annichila con un positrone
(elettrone) emettendo un secondo fotone.
|
|
|
 Incontriamo qui di passaggio un protagonista
delle teorie quantistiche di campo: la "particella virtuale". Mi
guardo bene dallo spiegare ora di che si tratta. Però i due punti a) e
b) di cui sopra fanno proprio intervenire un elettrone virtuale: quello che ha
emesso un fotone ma non si è ancora annichilato.
Incontriamo qui di passaggio un protagonista
delle teorie quantistiche di campo: la "particella virtuale". Mi
guardo bene dallo spiegare ora di che si tratta. Però i due punti a) e
b) di cui sopra fanno proprio intervenire un elettrone virtuale: quello che ha
emesso un fotone ma non si è ancora annichilato.
 Ora abbiamo davanti (noi no, a dire il vero:
ma quelli che hanno costruito la QED) il compito di ritrovare questi processi
che si vedono in natura (e molti altri di cui non ho parlato) attraverso una
teoria fisica precisa, che deve far entrare in ballo da una parte i fotoni,
ossia il campo e.m. quantizzato; dall'altra parte elettroni e positroni, che
per ora sappiamo solo che debbono aver a che fare con l'equazione di Dirac.
Ora abbiamo davanti (noi no, a dire il vero:
ma quelli che hanno costruito la QED) il compito di ritrovare questi processi
che si vedono in natura (e molti altri di cui non ho parlato) attraverso una
teoria fisica precisa, che deve far entrare in ballo da una parte i fotoni,
ossia il campo e.m. quantizzato; dall'altra parte elettroni e positroni, che
per ora sappiamo solo che debbono aver a che fare con l'equazione di Dirac.
 Ma c'è un problema: nel caso dei
fotoni, abbiamo visto che essi nascono in modo naturale dalla quantizzazione
del campo e.m., retto dalle equazioni di Maxwell. Ci sarà forse un
altro genere di campo, la cui quantizzazione darà luogo a elettroni e
positroni?
Ma c'è un problema: nel caso dei
fotoni, abbiamo visto che essi nascono in modo naturale dalla quantizzazione
del campo e.m., retto dalle equazioni di Maxwell. Ci sarà forse un
altro genere di campo, la cui quantizzazione darà luogo a elettroni e
positroni?
 D'altra parte l'equazione di Dirac
è
D'altra parte l'equazione di Dirac
è l'equazione degli elettroni e dei
positroni, ma dovrei meglio dire che è l'equazione che descrive il
comportamento di un singolo
l'equazione degli elettroni e dei
positroni, ma dovrei meglio dire che è l'equazione che descrive il
comportamento di un singolo elettrone o
positrone (per es. l'elettrone di un atomo d'idrogeno): da questa equazione
non si possono ricavare annichilazioni o creazioni di coppie.
elettrone o
positrone (per es. l'elettrone di un atomo d'idrogeno): da questa equazione
non si possono ricavare annichilazioni o creazioni di coppie.
 Che si deve fare?
Che si deve fare?
 Ecco l'idea: l'equazione di Dirac ha come
oggetto matematico una "funzione d'onda", più o meno come
l'equazione di Schrödinger. C'è una differenza, perché la
presenza dello spin e dei due tipi di particella richiede che si tratti di una
funzione d'onda "a 4 componenti", ma questo a noi importa poco:
ciò che conta è che è sempre una funzione dello spazio e
del tempo, come la psi di Schrödinger, ma anche come i campi e.m. delle
equazioni di Maxwell!
Ecco l'idea: l'equazione di Dirac ha come
oggetto matematico una "funzione d'onda", più o meno come
l'equazione di Schrödinger. C'è una differenza, perché la
presenza dello spin e dei due tipi di particella richiede che si tratti di una
funzione d'onda "a 4 componenti", ma questo a noi importa poco:
ciò che conta è che è sempre una funzione dello spazio e
del tempo, come la psi di Schrödinger, ma anche come i campi e.m. delle
equazioni di Maxwell!
 Allora perché non interpretare questa
funzione d'onda di Dirac come "campo degli elettroni e positroni", e
provare a quantizzarlo, come abbiamo fatto col campo e.m.?
Allora perché non interpretare questa
funzione d'onda di Dirac come "campo degli elettroni e positroni", e
provare a quantizzarlo, come abbiamo fatto col campo e.m.?
 Detto fatto... Ci sono, tanto per cambiare,
alcune questioni che bisogna risolvere, per es. come far intervenire il
principio di Pauli. Ma vi pare che i "cervelloni" che pensavano a
queste cose non avrebbero trovato la soluzione?
Detto fatto... Ci sono, tanto per cambiare,
alcune questioni che bisogna risolvere, per es. come far intervenire il
principio di Pauli. Ma vi pare che i "cervelloni" che pensavano a
queste cose non avrebbero trovato la soluzione?
 Infatti Dirac non aveva quasi finito di scrivere
la sua equazione, che già Jordan e Wigner (1928) avevano capito come
fare. Peccato che non possa spiegarlo (per chi sa già tutto: sto
parlando degli anticommutatori, of course
Infatti Dirac non aveva quasi finito di scrivere
la sua equazione, che già Jordan e Wigner (1928) avevano capito come
fare. Peccato che non possa spiegarlo (per chi sa già tutto: sto
parlando degli anticommutatori, of course ).
).
 Il resto è quasi facile: abbiamo
quantizzato il "campo di Dirac", e poiché questo nasce
già da una quantizzazione (la teoria quanto-relativistica di Dirac)
abbiamo fatto una "seconda quantizzazione".
Il resto è quasi facile: abbiamo
quantizzato il "campo di Dirac", e poiché questo nasce
già da una quantizzazione (la teoria quanto-relativistica di Dirac)
abbiamo fatto una "seconda quantizzazione".
 Se avete la sensazione di acrobati sul
trapezio e sulla fune, non vi sbagliate di tanto... La differenza è
solo che alla fine queste acrobazie intellettuali dovranno essere messe in
relazione col mondo reale... Vedremo.
Se avete la sensazione di acrobati sul
trapezio e sulla fune, non vi sbagliate di tanto... La differenza è
solo che alla fine queste acrobazie intellettuali dovranno essere messe in
relazione col mondo reale... Vedremo.
 Intanto è scontato che da questa
quantizzazione del campo di Dirac si ritrovano elettroni e positroni,
ovviamente coi loro bravi spin, ecc. ecc.
Intanto è scontato che da questa
quantizzazione del campo di Dirac si ritrovano elettroni e positroni,
ovviamente coi loro bravi spin, ecc. ecc.
 Stavo per scrivere "e cariche, e momenti
magnetici". Ma un momento! come si può misurare la carica o il
momento magnetico di un elettrone? Solo facendolo interagire con un campo,
elettrico o magnetico rispettivamente!
Stavo per scrivere "e cariche, e momenti
magnetici". Ma un momento! come si può misurare la carica o il
momento magnetico di un elettrone? Solo facendolo interagire con un campo,
elettrico o magnetico rispettivamente!
 Ma campo elettrico o magnetico significano
fotoni, quindi dobbiamo fare interagire le nostre particelle coi fotoni,
altrimenti niente carica, niente momento magnetico. Si può?
Ma campo elettrico o magnetico significano
fotoni, quindi dobbiamo fare interagire le nostre particelle coi fotoni,
altrimenti niente carica, niente momento magnetico. Si può?
 In realtà se lasciamo le cose a questo
punto la risposta è negativa. Avevo già fatto notare che la
quantizzazione del campo e.m. ci ha dato dei fotoni "liberi", senza
cariche con cui interagire; la quantizzazione del campo di Dirac fa lo stesso:
produce elettroni e positroni "liberi", cioè senza fotoni con
cui interagire (anzi, non interagiscono neppure fra loro: sono particelle
immaginarie, nel senso che differiscono da quelle del mondo che ci circonda
proprio per essere completamente prive d'interazioni).
In realtà se lasciamo le cose a questo
punto la risposta è negativa. Avevo già fatto notare che la
quantizzazione del campo e.m. ci ha dato dei fotoni "liberi", senza
cariche con cui interagire; la quantizzazione del campo di Dirac fa lo stesso:
produce elettroni e positroni "liberi", cioè senza fotoni con
cui interagire (anzi, non interagiscono neppure fra loro: sono particelle
immaginarie, nel senso che differiscono da quelle del mondo che ci circonda
proprio per essere completamente prive d'interazioni).
 Dunque il lavoro fatto è da buttar via?
Neppure per sogno, solo che bisogna introdurre le interazioni. Come? Alla
prossima puntata, naturalmente...
Dunque il lavoro fatto è da buttar via?
Neppure per sogno, solo che bisogna introdurre le interazioni. Come? Alla
prossima puntata, naturalmente...
(Fine della quarta puntata)
 Ma come mai i positroni non erano stati visti
prima? Che proprietà hanno?
Ma come mai i positroni non erano stati visti
prima? Che proprietà hanno? La risposta alla seconda domanda è molto
semplice: sono in tutto e per tutto uguali agli elettroni, salvo per il segno
della carica. In particolare, hanno la stessa massa, spin, momento
magnetico.
La risposta alla seconda domanda è molto
semplice: sono in tutto e per tutto uguali agli elettroni, salvo per il segno
della carica. In particolare, hanno la stessa massa, spin, momento
magnetico.
