Breve storia dell'elettrodinamica quantistica
Elio Fabri
Ultima revisione: 17-9-07
Ottava puntata
 Abbiamo incontrato nella scorsa puntata la
vera difficoltà di QED: le cosiddette "divergenze
ultraviolette". Divergenze, perché si tratta d'integrali che
divergono; ultraviolette perché le divergenze, ossia gli infiniti, sono
dovuti alle particelle virtuali di grande energia (piccola lunghezza
d'onda).
Abbiamo incontrato nella scorsa puntata la
vera difficoltà di QED: le cosiddette "divergenze
ultraviolette". Divergenze, perché si tratta d'integrali che
divergono; ultraviolette perché le divergenze, ossia gli infiniti, sono
dovuti alle particelle virtuali di grande energia (piccola lunghezza
d'onda).
 Per esorcizzare questo "diabolus" i
teorici si misero al lavoro, e pian piano cominciò ad apparire un po'
di luce. Finché negli anni 1946-48 (erano giusto 50 anni quando
ho cominciato a scrivere questa "breve" storia) Feynman,
Schwinger e Tomonaga riuscirono a dimostrare, indipendentemente tra loro, che
i responsabili delle divergenze erano solo tre diagrammi, tutti presenti nelle
figure che ho disegnato nella settima puntata, e che riporto qui accanto:
Per esorcizzare questo "diabolus" i
teorici si misero al lavoro, e pian piano cominciò ad apparire un po'
di luce. Finché negli anni 1946-48 (erano giusto 50 anni quando
ho cominciato a scrivere questa "breve" storia) Feynman,
Schwinger e Tomonaga riuscirono a dimostrare, indipendentemente tra loro, che
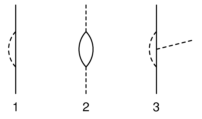
i responsabili delle divergenze erano solo tre diagrammi, tutti presenti nelle
figure che ho disegnato nella settima puntata, e che riporto qui accanto:
| 1) |
il fotone virtuale emesso e subito riassorbito da un elettrone
(fig. 1) |
| 2) |
la coppia virtuale prodotta da un fotone e subito annichilata
(fig. 2) |
| 3) |
il fotone virtuale emesso da un elettrone prima di emettere
o assorbire
un altro fotone, e riassorbito dopo (fig. 3). |
|  |
 Va detto che questi processi virtuali sono
possibili anche in casi semplicissimi, più semplici dell'effetto
Compton che abbiamo visto in precedenza.
Va detto che questi processi virtuali sono
possibili anche in casi semplicissimi, più semplici dell'effetto
Compton che abbiamo visto in precedenza.
 Pensiamo ad es. al processo 1. Questo
può avvenire anche con un elettrone libero, in quanto esso, per quanto
libero, non è privo d'interazione col campo e.m. Dunque un elettrone
che viaggia solo soletto non è mai "nudo", ma potrà
continuamente emettere e riassorbire fotoni virtuali. Si dimostra che questo
gioco ha un effetto importante sull'elettrone: ne altera l'energia di riposo,
ossia la massa.
Pensiamo ad es. al processo 1. Questo
può avvenire anche con un elettrone libero, in quanto esso, per quanto
libero, non è privo d'interazione col campo e.m. Dunque un elettrone
che viaggia solo soletto non è mai "nudo", ma potrà
continuamente emettere e riassorbire fotoni virtuali. Si dimostra che questo
gioco ha un effetto importante sull'elettrone: ne altera l'energia di riposo,
ossia la massa.
 Ma noi non possiamo osservare un elettrone
nudo, quindi la sua massa nuda ci è sconosciuta: quella che misuriamo
è sempre la massa di un elettrone "vestito" da tutte queste
particelle virtuali.
Ma noi non possiamo osservare un elettrone
nudo, quindi la sua massa nuda ci è sconosciuta: quella che misuriamo
è sempre la massa di un elettrone "vestito" da tutte queste
particelle virtuali.
 Il calcolo ci dice che la correzione alla
massa dell'elettrone sarebbe infinita; ma ci dice anche che questo succede se
consideriamo fotoni virtuali di energie comunque grandi (il che è
obbligatorio, stando alla meccanica quantistica). Perciò proviamo a
dimenticare per un momento questa regola, e limitiamoci a fotoni di energia
non superiore a un certo valore E,
Il calcolo ci dice che la correzione alla
massa dell'elettrone sarebbe infinita; ma ci dice anche che questo succede se
consideriamo fotoni virtuali di energie comunque grandi (il che è
obbligatorio, stando alla meccanica quantistica). Perciò proviamo a
dimenticare per un momento questa regola, e limitiamoci a fotoni di energia
non superiore a un certo valore E, molto
molto grande, ma finito: allora la correzione alla massa sarà anch'essa
finita.
molto
molto grande, ma finito: allora la correzione alla massa sarà anch'essa
finita.
 (Tanto per cambiare, qui e nel seguito sto
facendo una serie di semplificazioni e anche di distorsioni rispetto al reale
stato delle cose; ma temo non sia tanto facile essere più precisi e al
tempo stesso restare comprensibili ... ammesso che quello che sto scrivendo
sia comprensibile!)
(Tanto per cambiare, qui e nel seguito sto
facendo una serie di semplificazioni e anche di distorsioni rispetto al reale
stato delle cose; ma temo non sia tanto facile essere più precisi e al
tempo stesso restare comprensibili ... ammesso che quello che sto scrivendo
sia comprensibile!)
 In queste condizioni possiamo ragionare
all'indietro: noi non possiamo misurare la massa nuda, ma solo quella vestita?
Benissimo; proviamo a ipotizzare un valore per la massa nuda, calcoliamo la
massa vestita che ne risulta e confrontiamola con le misure. Non verrà
giusta, possiamo scommetterci; ma per tentativi potremo aggiustare la massa
nuda in modo che quelle vestita coincida col valore misurato. (In
realtà non è necessario procedere a tentoni: si tratta solo di
risolvere una certa equazione, in cui la massa nuda è l'incognita.)
In queste condizioni possiamo ragionare
all'indietro: noi non possiamo misurare la massa nuda, ma solo quella vestita?
Benissimo; proviamo a ipotizzare un valore per la massa nuda, calcoliamo la
massa vestita che ne risulta e confrontiamola con le misure. Non verrà
giusta, possiamo scommetterci; ma per tentativi potremo aggiustare la massa
nuda in modo che quelle vestita coincida col valore misurato. (In
realtà non è necessario procedere a tentoni: si tratta solo di
risolvere una certa equazione, in cui la massa nuda è l'incognita.)
 Un ragionamento simile si fa col diagramma
2, che viene descritto col termine "polarizzazione del vuoto". Vuol
dire che per un fotone lo spazio non è realmente vuoto, e che
può "polarizzarsi" al passaggio di un fotone, un po' come un
dielettrico si polarizza a causa di un campo elettrico statico.
Un ragionamento simile si fa col diagramma
2, che viene descritto col termine "polarizzazione del vuoto". Vuol
dire che per un fotone lo spazio non è realmente vuoto, e che
può "polarizzarsi" al passaggio di un fotone, un po' come un
dielettrico si polarizza a causa di un campo elettrico statico.
 C'è un effetto importante di questa
polarizzazione, ed è che la carica dell'elettrone ne viene alterata.
Succede un fenomeno analogo a quello visto con la massa, e lo si tratta allo
stesso modo: potremo limitarci a elettroni virtuali di energia non superiore a
E,
C'è un effetto importante di questa
polarizzazione, ed è che la carica dell'elettrone ne viene alterata.
Succede un fenomeno analogo a quello visto con la massa, e lo si tratta allo
stesso modo: potremo limitarci a elettroni virtuali di energia non superiore a
E, calcolare la correzione, da qui
ricavare quale carica nuda occorre usare per arrivare alla carica vestita:
quella che Millikan misurò agli inizi del secolo.
calcolare la correzione, da qui
ricavare quale carica nuda occorre usare per arrivare alla carica vestita:
quella che Millikan misurò agli inizi del secolo.
 Resterebbe infine il diagramma 3, che
però si riconduce all'1. Spiegare come e perché, va troppo al di
là di questa storia. Posso solo far notare che in certo senso si
somigliano: in entrambi c'è un fotone virtuale che nasce e poi muore...
Resterebbe infine il diagramma 3, che
però si riconduce all'1. Spiegare come e perché, va troppo al di
là di questa storia. Posso solo far notare che in certo senso si
somigliano: in entrambi c'è un fotone virtuale che nasce e poi muore...
 Ed ecco il colpo di bacchetta magica: tutti
i calcoli accennati fin qui non sono esatti, perché ci siamo limitati a
non andare oltre una certa energia E.
Ed ecco il colpo di bacchetta magica: tutti
i calcoli accennati fin qui non sono esatti, perché ci siamo limitati a
non andare oltre una certa energia E. Questo era necessario per non avere risultati infiniti. Ma se dopo aver
fatto le correzioni, ossia dopo aver espresso tutte le grandezze calcolabili
in termini della massa e della carica dell'elettrone "vestito",
mandiamo E
Questo era necessario per non avere risultati infiniti. Ma se dopo aver
fatto le correzioni, ossia dopo aver espresso tutte le grandezze calcolabili
in termini della massa e della carica dell'elettrone "vestito",
mandiamo E a infinito, il risultato del
calcolo resta finito e non contiene più parametri arbitrari o
inosservabili!
a infinito, il risultato del
calcolo resta finito e non contiene più parametri arbitrari o
inosservabili!
 In questo modo fu possibile calcolare le
correzioni di ordine superiore alle probabilità di molti processi
(ricordate ad es. l'effetto Compton?) e confrontare con i risultati degli
esperimenti.
In questo modo fu possibile calcolare le
correzioni di ordine superiore alle probabilità di molti processi
(ricordate ad es. l'effetto Compton?) e confrontare con i risultati degli
esperimenti.
 Uno degli esempi più significativi
è il seguente. Nella terza puntata ho parlato dello spin e del
momento magnetico dell'elettrone, e ho scritto che la teoria di Dirac, in
accordo con le misure, prevede fra le due grandezze il rapporto
e
Uno degli esempi più significativi
è il seguente. Nella terza puntata ho parlato dello spin e del
momento magnetico dell'elettrone, e ho scritto che la teoria di Dirac, in
accordo con le misure, prevede fra le due grandezze il rapporto
e /2mc.
/2mc. Anche QED1 (la teoria al primo ordine) dà lo stesso rapporto,
mentre il calcolo degli ordini superiori prevede una correzione: quel rapporto
va moltiplicato per 1.0011596525 (con l'ultima cifra un po' incerta,
perché anche i più raffinati calcoli numerici sono sempre
approssimati).
Anche QED1 (la teoria al primo ordine) dà lo stesso rapporto,
mentre il calcolo degli ordini superiori prevede una correzione: quel rapporto
va moltiplicato per 1.0011596525 (con l'ultima cifra un po' incerta,
perché anche i più raffinati calcoli numerici sono sempre
approssimati).
 Bene: mentre i teorici calcolavano, gli
sperimentali misuravano, e il loro responso fu 1.0011596522, con errore
inferiore all'ultima cifra scritta. Non occorrono commenti, mi pare...
Bene: mentre i teorici calcolavano, gli
sperimentali misuravano, e il loro responso fu 1.0011596522, con errore
inferiore all'ultima cifra scritta. Non occorrono commenti, mi pare...
 C'è solo da aggiungere che
tutti
C'è solo da aggiungere che
tutti i calcoli fatti con QED hanno dato
risultati dello stesso genere, ossia in eccellente accordo con gli
esperimenti. Non esiste nessuna teoria, nell'ambito della fisica delle
interazioni fondamentali, che mostri un così perfetto e generale
accordo con le misure.
i calcoli fatti con QED hanno dato
risultati dello stesso genere, ossia in eccellente accordo con gli
esperimenti. Non esiste nessuna teoria, nell'ambito della fisica delle
interazioni fondamentali, che mostri un così perfetto e generale
accordo con le misure.
 Non vi stupirete se a Feynman, Schwinger e
Tomonaga è stato assegnato il Nobel...
Non vi stupirete se a Feynman, Schwinger e
Tomonaga è stato assegnato il Nobel...
 Allora siamo a posto? chiederete a
questo punto; la storia è finita? Non è finita, per varie
ragioni...
Allora siamo a posto? chiederete a
questo punto; la storia è finita? Non è finita, per varie
ragioni...
 Lo vedremo nella prossima puntata, che
sarà anche l'ultima.
Lo vedremo nella prossima puntata, che
sarà anche l'ultima.
(Fine dell'ottava puntata)
 Abbiamo incontrato nella scorsa puntata la
vera difficoltà di QED: le cosiddette "divergenze
ultraviolette". Divergenze, perché si tratta d'integrali che
divergono; ultraviolette perché le divergenze, ossia gli infiniti, sono
dovuti alle particelle virtuali di grande energia (piccola lunghezza
d'onda).
Abbiamo incontrato nella scorsa puntata la
vera difficoltà di QED: le cosiddette "divergenze
ultraviolette". Divergenze, perché si tratta d'integrali che
divergono; ultraviolette perché le divergenze, ossia gli infiniti, sono
dovuti alle particelle virtuali di grande energia (piccola lunghezza
d'onda). Per esorcizzare questo "diabolus" i
teorici si misero al lavoro, e pian piano cominciò ad apparire un po'
di luce. Finché negli anni 1946-48 (erano giusto 50 anni quando
ho cominciato a scrivere questa "breve" storia) Feynman,
Schwinger e Tomonaga riuscirono a dimostrare, indipendentemente tra loro, che
i responsabili delle divergenze erano solo tre diagrammi, tutti presenti nelle
figure che ho disegnato nella settima puntata, e che riporto qui accanto:
Per esorcizzare questo "diabolus" i
teorici si misero al lavoro, e pian piano cominciò ad apparire un po'
di luce. Finché negli anni 1946-48 (erano giusto 50 anni quando
ho cominciato a scrivere questa "breve" storia) Feynman,
Schwinger e Tomonaga riuscirono a dimostrare, indipendentemente tra loro, che
i responsabili delle divergenze erano solo tre diagrammi, tutti presenti nelle
figure che ho disegnato nella settima puntata, e che riporto qui accanto:
